题目内容
14．A，B两人下棋，A获胜的概率为30%，两人下成和棋的概率为20%，那么A不输的概率为0.5．分析 利用互斥事件的概率加法公式即可得出．
解答 解：∵A不输与A、B两人下成和棋是互斥事件．
∴根据互斥事件的概率计算公式可知：A不输的概率P=0.2+0.3=0.5．
故答案为：O.5．
点评 此题主要考查了概率的意义，正确理解互斥事件及其概率加法公式是解题的关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
4．
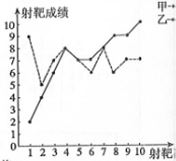甲、乙两人在相同的条件下各射靶10次，每次射靶成绩均为整数（单位：环），如图所示
（Ⅰ）填写下表：
（Ⅱ）请从四个不同的角度对这次测试进行分析：
①从平均数与方差相结合的角度分析偏离程度；
②从平均数与中位数相结合的角度分析谁的成绩好些；
③从平均数和命中9环以上的次数看谁的成绩好些；
④从折线图上两人射击命中环数及走势分析谁更有潜力．
甲、乙两人在相同的条件下各射靶10次，每次射靶成绩均为整数（单位：环），如图所示（Ⅰ）填写下表：
| 平均数 | 方差 | 中位数 | 命中9环及以上 | |
| 甲 | 1.2 | 7 | ||
| 乙 | 3 |
①从平均数与方差相结合的角度分析偏离程度；
②从平均数与中位数相结合的角度分析谁的成绩好些；
③从平均数和命中9环以上的次数看谁的成绩好些；
④从折线图上两人射击命中环数及走势分析谁更有潜力．
5．若a＞b，则下列不等式成立的是（ ）
| A． | algx＞blgx（x＞0） | B． | ax2＞bx2 | C． | a2＞b2 | D． | $\frac{a}{{{2^x}+1}}＞\frac{b}{{{2^x}+1}}$ |
9．圆x2+y2+2x-2y+1=0关于直线x-y+3=0对称圆的方程为（ ）
| A． | （x-1）2+（y+1）2=1 | B． | （x+2）2+（y-2）2=1 | C． | （x+1）2+（y-1）2=1 | D． | （x-2）2+（y+2）2=1 |