题目内容
4．由直线y=0，x=e，y=2x及曲线$y=\frac{2}{x}$所围成的封闭的图形的面积为（ ）| A． | 3+2ln2 | B． | 3 | C． | 2e2-3 | D． | e |
分析 首先由题意画出图形，明确围成的封闭图形用定积分表示，然后求定积分．
解答 解：由题意，直线y=0，x=e，y=2x及曲线y=$\frac{2}{x}$所围成的封闭的图形如图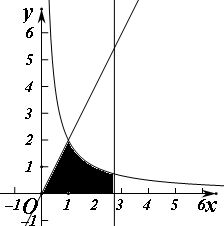
直线y=2x与曲线y=$\frac{2}{x}$的交点为（1，2），
所以阴影部分的面积为：${∫}_{0}^{1}2xdx+{∫}_{1}^{e}\frac{2}{x}dx$=x2|${\;}_{0}^{1}$+2lnx|${\;}_{1}^{e}$=3
故选B
点评 本题考查了利用定积分求曲边梯形的面积；关键是明确利用定积分表示围成的面积．
练习册系列答案
相关题目
16．已知集合A={x|2＜x＜4}，B={x||x-1|≥2}，则A∩B=（ ）
| A． | （3，4） | B． | （2，3] | C． | [3，4） | D． | （2，3） |
13．某同学在研究性学习中，收集到某制药厂今年2-6月甲胶囊产量（单位：千盒）的数据如表所示：
若该同学用最小二乘法求线性回归方程，则可预测得该厂10月份生产的甲胶囊为12.38千盒．
参考数据：22+32+42+52+62=90，2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3．
| 月份x | 2 | 3 | 4 | 5 | 6 |
| y（千盒） | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
参考数据：22+32+42+52+62=90，2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3．
14．下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x（吨）与相应的生产能耗y （吨）的4组对应数据：
若通过上表的4组数据，得到y关于x的线性回归方程为$\stackrel{∧}{y}$=0.7x+0.35，那么表中t的值应为2.8．
| x | 2 | 4 | 5 | 7 |
| y | 1.5 | t | 4.2 | 5.5 |