题目内容
三角形的两边长分别为1，
，第三边上的中线长为1，则此三角形外接圆半径为______．
| 3 |
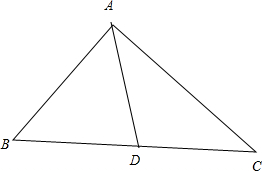
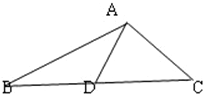
设AB=1，AC=
，AD=1，D为BC边的中点，BC=2x，
则BD=DC=x，
△ABD中，由余弦定理可得cos∠ADB=
，
△ADC中，由余弦定理可得，cos∠ADC=
，
因为cos∠ADB=-cos∠ADC
所以
=-
∴x=1
∴BC=2
∴AB2+AC2=BC2即A=90°
∴外接圆的直径2R=BC=2，从而可得R=1
故答案为：1．
| 3 |
则BD=DC=x，
△ABD中，由余弦定理可得cos∠ADB=
| 12+x2-12 |
| 2x |
△ADC中，由余弦定理可得，cos∠ADC=
12+x2-(
| ||
| 2x |
因为cos∠ADB=-cos∠ADC
所以
| 12+x2-12 |
| 2x |
12+x2-(
| ||
| 2x |
∴x=1
∴BC=2
∴AB2+AC2=BC2即A=90°
∴外接圆的直径2R=BC=2，从而可得R=1
故答案为：1．
练习册系列答案
相关题目
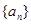的前
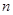项和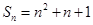
，
时，数列{an}为递减数列；②当
为正整数时，数列{an}必有两项相等的最大项