ĚâÄżÄÚČÝ
ˇľĚâÄżˇżĽşÖŞÔ˛F1Łş(x+1)2 +y2= r2(1ˇÜrˇÜ3)Ł¬Ô˛F2Łş(x-1)2+y2= (4-r)2Ł®
Ł¨1Ł©Ö¤Ă÷ŁşÔ˛F1ÓëÔ˛F2ÓĐą«ą˛µăŁ¬˛˘Çóą«ą˛µăµÄąěĽŁEµÄ·˝łĚŁ»
Ł¨2Ł©ŇŃÖŞµăQ(mŁ¬0)(m<0)Ł¬ąýµăEбÂĘÎŞk(kˇŮ0Ł©µÄÖ±ĎßÓ루˘ńŁ©Öй켣EĎŕ˝»ÓÚMŁ¬NÁ˝µăŁ¬ĽÇÖ±ĎßQMµÄбÂĘÎŞk1Ł¬Ö±ĎßQNµÄбÂĘÎŞk2Ł¬ĘÇ·ń´ćÔÚʵĘýmĘąµĂk(k1+k2)ÎŞ¶¨ÖµŁżČô´ćÔÚŁ¬ÇółömµÄÖµŁ¬Čô˛»´ćÔÚŁ¬ËµĂ÷ŔíÓÉŁ®
ˇľ´đ°¸ˇżŁ¨1Ł©Ľű˝âÎöŁ¬![]() Ł¨2Ł©´ćÔÚŁ¬
Ł¨2Ł©´ćÔÚŁ¬![]()
ˇľ˝âÎöˇż
Ł¨1Ł©ÇółöÔ˛![]() şÍÔ˛
şÍÔ˛![]() µÄÔ˛ĐĺͰ뾶Ł¬Í¨ąýÔ˛F1ÓëÔ˛F2ÓĐą«ą˛µăÇółö
µÄÔ˛ĐĺͰ뾶Ł¬Í¨ąýÔ˛F1ÓëÔ˛F2ÓĐą«ą˛µăÇółö![]() µÄ·¶Î§Ł¬´Ó¶ř¸ůľÝ
µÄ·¶Î§Ł¬´Ó¶ř¸ůľÝ![]() żÉµĂ
żÉµĂ![]() µăµÄąěĽŁŁ¬˝ř¶řÇółö·˝łĚŁ»
µăµÄąěĽŁŁ¬˝ř¶řÇółö·˝łĚŁ»
Ł¨2Ł©ąý![]() µăÇŇбÂĘÎŞ
µăÇŇбÂĘÎŞ![]() µÄÖ±Ďß·˝łĚÎŞ
µÄÖ±Ďß·˝łĚÎŞ![]() Ł¬Éč
Ł¬Éč![]() Ł¬
Ł¬![]() Ł¬ÁŞÁ˘Ö±Ďß·˝łĚşÍÍÖÔ˛·˝łĚŁ¬¸ůľÝΤ´ď¶¨ŔíŇÔĽ°
Ł¬ÁŞÁ˘Ö±Ďß·˝łĚşÍÍÖÔ˛·˝łĚŁ¬¸ůľÝΤ´ď¶¨ŔíŇÔĽ°![]() Ł¬
Ł¬![]() Ł¬żÉµĂ
Ł¬żÉµĂ![]() Ł¬¸ůľÝĆäÎŞ¶¨ÖµŁ¬ÔňÓĐ
Ł¬¸ůľÝĆäÎŞ¶¨ÖµŁ¬ÔňÓĐ![]() Ł¬˝ř¶řżÉµĂ˝áąű.
Ł¬˝ř¶řżÉµĂ˝áąű.
Ł¨1Ł©ŇňÎŞ![]() Ł¬
Ł¬![]() Ł¬ËůŇÔ
Ł¬ËůŇÔ![]() Ł¬
Ł¬
ŇňÎŞÔ˛![]() µÄ°ëľ¶ÎŞ
µÄ°ëľ¶ÎŞ![]() Ł¬Ô˛
Ł¬Ô˛![]() µÄ°ëľ¶ÎŞ
µÄ°ëľ¶ÎŞ![]() Ł¬
Ł¬
ÓÖŇňÎŞ![]() Ł¬ËůŇÔ
Ł¬ËůŇÔ![]() Ł¬Ľ´
Ł¬Ľ´![]() Ł¬
Ł¬
ËůŇÔÔ˛![]() ÓëÔ˛
ÓëÔ˛![]() ÓĐą«ą˛µăŁ¬
ÓĐą«ą˛µăŁ¬
Éčą«ą˛µăÎŞ![]() Ł¬Ňň´Ë
Ł¬Ňň´Ë![]() Ł¬ËůŇÔ
Ł¬ËůŇÔ![]() µăµÄąěĽŁ
µăµÄąěĽŁ![]() ĘÇŇÔ
ĘÇŇÔ![]() Ł¬
Ł¬![]() ÎŞ˝ąµăµÄÍÖÔ˛Ł¬
ÎŞ˝ąµăµÄÍÖÔ˛Ł¬
ËůŇÔ![]() Ł¬
Ł¬![]() Ł¬
Ł¬![]() Ł¬
Ł¬
Ľ´ąěĽŁ![]() µÄ·˝łĚÎŞ
µÄ·˝łĚÎŞ![]() Ł»
Ł»
Ł¨2Ł©ąý![]() µăÇŇбÂĘÎŞ
µăÇŇбÂĘÎŞ![]() µÄÖ±Ďß·˝łĚÎŞ
µÄÖ±Ďß·˝łĚÎŞ![]() Ł¬Éč
Ł¬Éč![]() Ł¬
Ł¬![]()
ÓÉ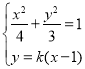 ĎűČĄ
ĎűČĄ![]() µĂµ˝
µĂµ˝![]() Ł¬
Ł¬
Ôň![]() Ł¬
Ł¬![]() Ł¬ ˘Ů
Ł¬ ˘Ů
ŇňÎŞ![]() Ł¬
Ł¬![]() Ł¬
Ł¬
ËůŇÔ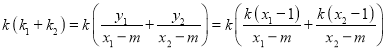
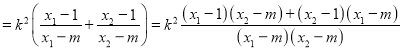
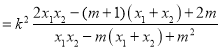 Ł¬
Ł¬
˝«˘ŮĘ˝´úČëŐűŔíµĂ![]()
ŇňÎŞ![]() Ł¬
Ł¬
ËůŇÔµ±![]() ʱŁ¬Ľ´
ʱŁ¬Ľ´![]() ʱŁ¬
ʱŁ¬![]() .
.
Ľ´´ćÔÚʵĘý![]() ĘąµĂ
ĘąµĂ![]() .
.