题目内容
已知函数y=f(x)的定义域为R,当x<0时,f(x)>1,且对任意的实数x,y,等式f(x)+f(y)=f(x+y)恒成立,若数列{an}满足a1=f(0),且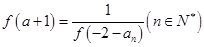 ,则a2011的值为
,则a2011的值为
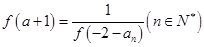 ,则a2011的值为
,则a2011的值为| A.4017 | B.4018 | C.4019 | D.4021 |
D
因为是选择题,可用特殊函数来研究,根据条件,底数小于1的指数函数符合题意,可令f(x)=(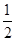 )x,从而很容易地求得则a1=f(0)=1,再由 f(an+1)=
)x,从而很容易地求得则a1=f(0)=1,再由 f(an+1)=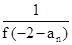 (n∈N*),得到an+1=an+2,由等差数列的定义求得结果.
(n∈N*),得到an+1=an+2,由等差数列的定义求得结果.
解:根据题意,不妨设f(x)=(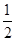 )x
)x
则a1=f(0)=1,
∵f(an+1)=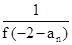 (n∈N*),
(n∈N*),
∴an+1=an+2
∴数列{an}是以1为首项,以2为公差的等差数列
∴an=2n-1
∴a2011=4021
故选D
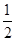 )x,从而很容易地求得则a1=f(0)=1,再由 f(an+1)=
)x,从而很容易地求得则a1=f(0)=1,再由 f(an+1)=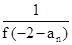 (n∈N*),得到an+1=an+2,由等差数列的定义求得结果.
(n∈N*),得到an+1=an+2,由等差数列的定义求得结果.解:根据题意,不妨设f(x)=(
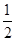 )x
)x则a1=f(0)=1,
∵f(an+1)=
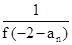 (n∈N*),
(n∈N*),∴an+1=an+2
∴数列{an}是以1为首项,以2为公差的等差数列
∴an=2n-1
∴a2011=4021
故选D

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 第
第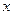 天
天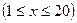 的销售价格
的销售价格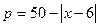 (元∕百斤),一农户在第
(元∕百斤),一农户在第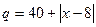 (百斤)。
(百斤)。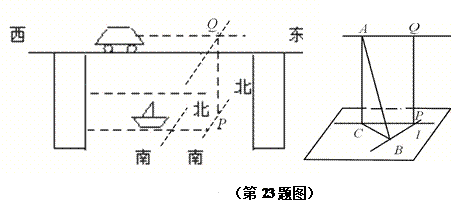
 本小题满分12分)
本小题满分12分) (单位:万元)随销售利润
(单位:万元)随销售利润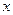 (单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的
(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的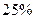 ,现有三个奖励模型:
,现有三个奖励模型: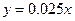 ,
,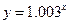 ,
,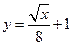 ,问其中是否有模型能完全符合公司的要求?说明理由.(参考数据:
,问其中是否有模型能完全符合公司的要求?说明理由.(参考数据: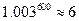 )
)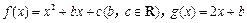 ,且对于任意
,且对于任意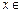 R,恒有
R,恒有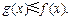
 ;
;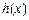 满足:
满足: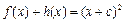 ,证明:函数
,证明:函数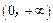 内没有零点.
内没有零点.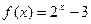 的零点所在的区间为( )
的零点所在的区间为( )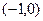
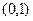
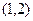
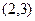
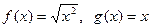
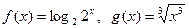
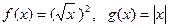
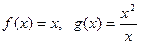
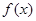 的值域是其定义域的子集,那么
的值域是其定义域的子集,那么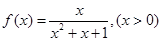 , ②
, ②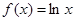
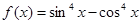
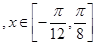 , ④
, ④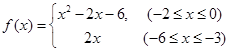
 (请把符合
(请把符合 条件的序号全部填在横线上)
条件的序号全部填在横线上)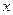 的方程
的方程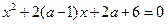 有一正一负两实根,实数
有一正一负两实根,实数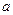 取值范围__
取值范围__