题目内容
【题目】已知等比数列{an}的公比q,前n项的和Sn , 对任意的n∈N* , Sn>0恒成立,则公比q的取值范围是 .
【答案】(﹣1,0)∪(0,+∞)
【解析】解:q≠1时,有Sn= ![]() , ∵Sn>0,∴a1>0,
, ∵Sn>0,∴a1>0,
则 ![]() >0恒成立,①当q>1时,1﹣qn<0恒成立,即qn>1恒成立,由q>1,知qn>1成立;②当q=1时,只要a1>0,Sn>0就一定成立;③当q<1时,需1﹣qn>0恒成立,
>0恒成立,①当q>1时,1﹣qn<0恒成立,即qn>1恒成立,由q>1,知qn>1成立;②当q=1时,只要a1>0,Sn>0就一定成立;③当q<1时,需1﹣qn>0恒成立,
当0<q<1时,1﹣qn>0恒成立,
当﹣1<q<0时,1﹣qn>0也恒成立,
当q<﹣1时,当n为偶数时,1﹣qn>0不成立,
当q=﹣1时,1﹣qn>0也不可能恒成立,
所以q的取值范围为(﹣1,0)∪(0,+∞).
所以答案是:(﹣1,0)∪(0,+∞).
【考点精析】解答此题的关键在于理解等比数列的前n项和公式的相关知识,掌握前![]() 项和公式:
项和公式: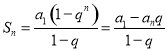 .
.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目