题目内容
(2013•重庆)设数列{an}满足:a1=1,an+1=3an,n∈N+.
(1)求{an}的通项公式及前n项和Sn;
(2)已知{bn}是等差数列,Tn为前n项和,且b1=a2,b3=a1+a2+a3,求T20.
(1)求{an}的通项公式及前n项和Sn;
(2)已知{bn}是等差数列,Tn为前n项和,且b1=a2,b3=a1+a2+a3,求T20.
(1)Sn= (2)1010
(2)1010
 (2)1010
(2)1010(1)由题意可得数列{an}是首项为1,公比为3的等比数列,
故可得an=1×3n﹣1=3n﹣1,
由求和公式可得Sn= =
= ;
;
(2)由题意可知b1=a2=3,b3=a1+a2+a3=1+3+9=13,
设数列{bn}的公差为d,可得b3﹣b1=10=2d,解得d=5
故T20=20×3+ =1010
=1010
故可得an=1×3n﹣1=3n﹣1,
由求和公式可得Sn=
 =
= ;
;(2)由题意可知b1=a2=3,b3=a1+a2+a3=1+3+9=13,
设数列{bn}的公差为d,可得b3﹣b1=10=2d,解得d=5
故T20=20×3+
 =1010
=1010
练习册系列答案
相关题目
 和
和 的通项公式分别为
的通项公式分别为 ,
, .将
.将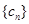 .
. ,
, ,
, ,
, 的值,并由此归纳数列
的值,并由此归纳数列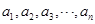 为
为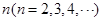 阶“期待数列”:
阶“期待数列”: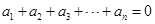 ,②
,②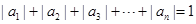 .
.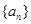 为
为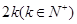 阶“期待数列”,求公比
阶“期待数列”,求公比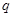 ;
;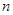 阶“期待数列”
阶“期待数列”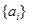 的前
的前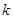 项和为
项和为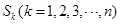 .
.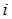 )求证:
)求证: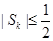 ;
;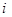
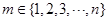 ,使
,使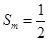 ,试问数列
,试问数列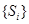
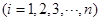 是否为
是否为 .
. 是首项
是首项 ,公比为
,公比为 的等比数列,
的等比数列,

 满足
满足 ,
, 表示
表示 项之积,则
项之积,则 = ( )
= ( )