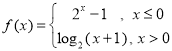题目内容
【题目】如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=![]() ,|AF2|=
,|AF2|=![]() .
.
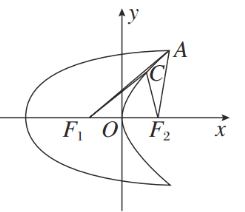
(1)求曲线C1和C2的方程;
(2)设点C是C2上一点,若|CF1|=![]() |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.
【答案】(1)曲线C1的方程为![]() +
+![]() =1(-3≤x≤
=1(-3≤x≤![]() ),曲线C2的方程为y2=4x(0≤x≤
),曲线C2的方程为y2=4x(0≤x≤![]() )
)
(2)2
【解析】(1)设椭圆方程为![]() +
+![]() =1(a>b>0),则2a=|AF1|+|AF2|=
=1(a>b>0),则2a=|AF1|+|AF2|=![]() +
+![]() =6,得a=3.
=6,得a=3.
设A(x,y),F1(-c,0),F2(c,0),则(x+c)2+y2=(![]() )2,(x-c)2+y2=(
)2,(x-c)2+y2=(![]() )2,两式相减得xc=
)2,两式相减得xc=![]() .由抛物线的定义可知|AF2|=x+c=
.由抛物线的定义可知|AF2|=x+c=![]() ,
,
则c=1,x=![]() 或x=1,c=
或x=1,c=![]() .又∠AF2F1为钝角,
.又∠AF2F1为钝角,
则x=1,c=![]() 不合题意,舍去.当c=1时,b=2
不合题意,舍去.当c=1时,b=2![]() ,
,
所以曲线C1的方程为![]() +
+![]() =1(-3≤x≤
=1(-3≤x≤![]() ),曲线C2的方程为y2=4x(0≤x≤
),曲线C2的方程为y2=4x(0≤x≤![]() ).
).
(2)过点F1作直线l垂直于x轴,过点C作CC1⊥l于点C1,依题意知|CC1|=|CF2|.
在Rt△CC1F1中,|CF1|=![]() |CF2|=
|CF2|=![]() |CC1|,所以∠C1CF1=45°,
|CC1|,所以∠C1CF1=45°,
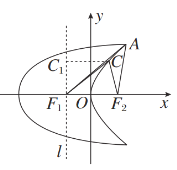
所以∠CF1F2=∠C1CF1=45°.
在△CF1F2中,设|CF2|=r,则|CF1|=![]() r,|F1F2|=2.
r,|F1F2|=2.
由余弦定理得22+(![]() r)2-2×2×
r)2-2×2×![]() rcos45°=r2,
rcos45°=r2,
解得r=2,
所以△CF1F2的面积S△CF1F2=![]() |F1F2|·|CF1|sin45°=
|F1F2|·|CF1|sin45°=![]() ×2×2
×2×2![]() sin45°=2.
sin45°=2.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目