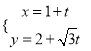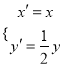题目内容
【题目】已知由自然数组成的![]() 元集合
元集合![]() ,非空集合
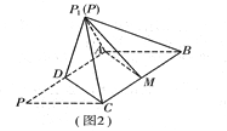
,非空集合![]() ,且对任意的
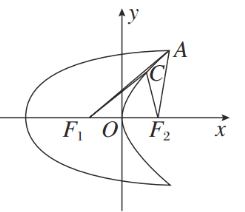
,且对任意的![]() ,都有
,都有![]() .
.
(1)当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() ;
;
(2)当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() 的元素总和;
的元素总和;
(3)定义一个集合的“交替和”如下:按照递减的次序重新排列该集合的元素,然后从最大数开始交替地减、加后继的数.例如集合![]() 的交替和是
的交替和是![]() ,集合
,集合![]() 的交替和为
的交替和为![]() .当
.当![]() 时,求所有满足条件的集合
时,求所有满足条件的集合![]() 的“交替和”的总和.
的“交替和”的总和.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)确定![]() 后可知
后可知![]() 有偶数个元素,分别讨论两个元素和四个元素的情况即可得到结果;
有偶数个元素,分别讨论两个元素和四个元素的情况即可得到结果;
(2)确定![]() 可知
可知![]() 有偶数个元素,分别在两个、四个、六个和八个元素的情况下求解元素之和,加和得到结果;
有偶数个元素,分别在两个、四个、六个和八个元素的情况下求解元素之和,加和得到结果;
(3)由![]() 、
、![]() 和
和![]() 时交替和总和的规律可得到当
时交替和总和的规律可得到当![]() 时,交替和总和为
时,交替和总和为![]() ,代入
,代入![]() 即可求得结果.
即可求得结果.
(1)当![]() 时,
时,![]()
![]() 是
是![]() 的非空子集,且
的非空子集,且![]() 时,
时,![]()
![]()
![]() 中有偶数个元素
中有偶数个元素
![]() 中有两个元素时,
中有两个元素时,![]() 或
或![]()
![]() 中有四个元素时,
中有四个元素时,![]()
![]() 所有满足条件的集合
所有满足条件的集合![]() 有:
有:![]() ,
,![]() ,
,![]()
(2)当![]() 时,
时,![]()
![]() 是
是![]() 的非空子集,且
的非空子集,且![]() 时,
时,![]()
![]()
![]() 中有偶数个元素
中有偶数个元素
当![]() 中有两个元素时,元素之和为:
中有两个元素时,元素之和为:![]()
当![]() 中有四个元素时,元素之和为:
中有四个元素时,元素之和为:![]()
当![]() 中有六个元素时,元素之和为:
中有六个元素时,元素之和为:![]()
当![]() 中有八个元素时,元素之和为:
中有八个元素时,元素之和为:![]()
![]() 所有满足条件的集合
所有满足条件的集合![]() 的元素总和为:
的元素总和为:![]()
(3)当![]() ,
,![]() ,交替和的总和为:
,交替和的总和为:![]()
当![]() 时,由(1)知,交替和的总和为:
时,由(1)知,交替和的总和为:![]()
当![]() 时,
时,![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() ,交替和的总和为:
,交替和的总和为:![]()
……以此类推,当![]() 时,交替和的总和为:
时,交替和的总和为:![]()
当![]() 时,
时,![]()
![]() 所求交替和的总和为:
所求交替和的总和为:![]()

练习册系列答案
相关题目