题目内容
已知f(n)=
+
+…+
(n∈N*),则下列结论正确的是( )
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
A.f(1)=
| ||||||
B.f(k+1)-f(k)=
| ||||||
C.f(2)=
| ||||||
D.f(k+1)-f(k)=
|
∵f(n)=
+
+…+
(n∈N*),
∴f(1)=
+
=
,f(2)=
+
+
+
+
,f(k+1)-f(k)=
+
+…+
-(
+
+…+
)=
+
-
.
故选D.
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
∴f(1)=
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 3(k+1) |
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| 3k |
| 1 |
| 3k+1 |
| 1 |
| 3k+2 |
| 2 |
| 3k+3 |
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 试用反证法证明三条抛物线中至少有一条与x轴的交点不只一个。
试用反证法证明三条抛物线中至少有一条与x轴的交点不只一个。
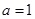 ”是“复数
”是“复数 (
( ,i为虚数单位)是纯虚数”的( )
,i为虚数单位)是纯虚数”的( ) (
( 为虚单位),则
为虚单位),则 的模
的模 = 。
= 。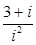 (
(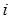 为虚数单位)的实部等于_________.
为虚数单位)的实部等于_________. 求证:
求证: