题目内容
19.已知a>b>0,椭圆C1方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,双曲线C2的方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1,C1与C2离心率之积为$\frac{\sqrt{3}}{2}$,则C2的渐近线方程为( )| A. | $\sqrt{2}$x±y=0 | B. | x±2y=0 | C. | x±$\sqrt{2}$y=0 | D. | 2x±y=0 |
分析 运用椭圆和双曲线的离心率公式,可得a,b的方程,再由双曲线的渐近线方程,即可得到结论.
解答 解:圆C1方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1的离心率为e1=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$,
双曲线C2的方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1的离心率为e2=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$,
由题意可得$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$•$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$=$\frac{\sqrt{3}}{2}$,
可得a2=2b2,即为a=$\sqrt{2}$b,
即有双曲线的渐近线方程为y=±$\frac{b}{a}$x,
则为x$±\sqrt{2}$y=0,
故选C.
点评 本题考查椭圆和双曲线的方程和性质,主要考查离心率和渐近线方程的求法,考查运算能力,属于易错题.

练习册系列答案
相关题目
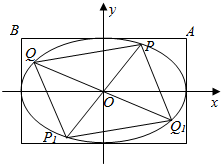 已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4
已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4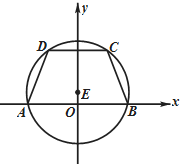 如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.
如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.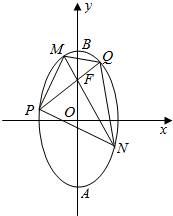 如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.
如图所示,椭圆长轴端点为点A、B、O为椭圆的中心,F为椭圆的上焦点,且$\overrightarrow{AF}•\overrightarrow{FB}=1,|\overrightarrow{OF}|=1$.