题目内容
16.设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{1}{2}$,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)( )| A. | 必在圆x2+y2=2上 | B. | 必在圆x2+y2=2外 | ||
| C. | 必在圆x2+y2=2内 | D. | 以上三种情形都有可能 |
分析 通过e=$\frac{1}{2}$可得$\frac{b}{a}$=$\frac{\sqrt{3}}{2}$,利用韦达定理可得x1+x2=-$\frac{\sqrt{3}}{2}$、x1x2=-$\frac{1}{2}$,根据完全平方公式、点与圆的位置关系计算即得结论.
解答 解:∵e=$\frac{c}{a}$=$\frac{1}{2}$,∴$\frac{b}{a}$=$\frac{\sqrt{3}}{2}$,
∵x1,x2是方程ax2+bx-c=0的两个实根,
∴由韦达定理:x1+x2=-$\frac{b}{a}$=-$\frac{\sqrt{3}}{2}$,x1x2=$\frac{-c}{a}$=-$\frac{1}{2}$,
∴x12+x22=(x1+x2)2-2x1x2=$\frac{3}{4}$+1=$\frac{7}{4}$<2,
∴点P(x1,x2)必在圆x2+y2=2内.
故选:C.
点评 本题考查椭圆的基本性质,考查点与圆的位置关系,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
5.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F,若F关于直线$\sqrt{3}$x+y=0的对称点A是椭圆C上的点,则椭圆C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$一l |
6.如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,A1A=2,则直线BC1到平面D1AC的距离为( )
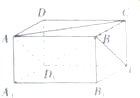

| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
 已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4
已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4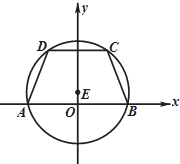 如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.
如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.