题目内容
(本小题满分14分)
已知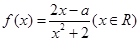
(1)当 时,求曲线
时,求曲线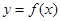 在点
在点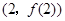 处的切线方程;
处的切线方程;
(2)若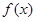 在区间
在区间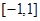 上是增函数,求实数
上是增函数,求实数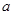 的取值范围
的取值范围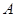 ;
;
(3)在(2)的条件下,设关于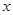 的方程
的方程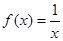 的两个根为
的两个根为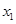 、
、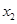 ,若对任意
,若对任意
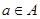 ,
,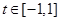 ,不等式
,不等式 恒成立,求
恒成立,求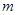 的取值范围.
的取值范围.
已知
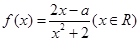
(1)当
 时,求曲线
时,求曲线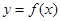 在点
在点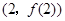 处的切线方程;
处的切线方程;(2)若
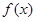 在区间
在区间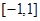 上是增函数,求实数
上是增函数,求实数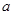 的取值范围
的取值范围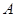 ;
;(3)在(2)的条件下,设关于
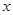 的方程
的方程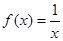 的两个根为
的两个根为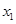 、
、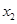 ,若对任意
,若对任意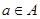 ,
,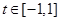 ,不等式
,不等式 恒成立,求
恒成立,求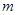 的取值范围.
的取值范围. 解:(1) y=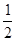 ;(2)
;(2)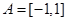 ;(3)
;(3)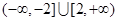 。
。
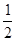 ;(2)
;(2)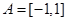 ;(3)
;(3)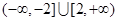 。
。本试题主要是考查了导数在研究函数中的运用。
(1)a=1时,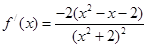 ,
, 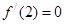 ,过点
,过点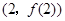 的切线方程为y=
的切线方程为y=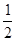 得到结论。
得到结论。
(2)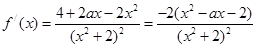 , ∵
, ∵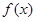 在区间
在区间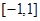 上是增函数,∴
上是增函数,∴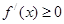 对
对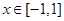 恒成立,即
恒成立,即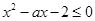 对
对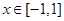 恒成立等价转化得到结论。
恒成立等价转化得到结论。
(3)由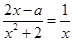 ,得
,得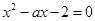 ,
,
∵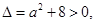 ∴
∴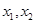 是方程
是方程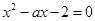 的两非零实根,
的两非零实根,
∴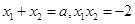 ,从而
,从而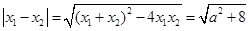
结合不等式得到结论。
解:(1)a=1时,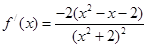 ,-------2分
,-------2分
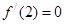 ,过点
,过点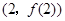 的切线方程为y=
的切线方程为y=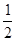 ----------4分
----------4分
(2)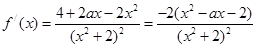 ,
,
∵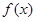 在区间
在区间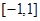 上是增函数,
上是增函数,
∴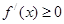 对
对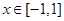 恒成立,
恒成立,
即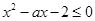 对
对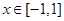 恒成立
恒成立
设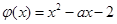 ,则问题等价于
,则问题等价于
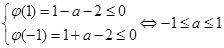 ,
,
∴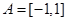 --------9
--------9
(3)由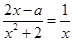 ,得
,得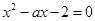 ,
,
∵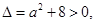 ∴
∴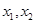 是方程
是方程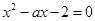 的两非零实根,
的两非零实根,
∴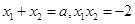 ,从而
,从而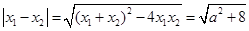 ,
,
∵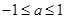 ,∴
,∴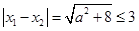 .
.
∴不等式 对任意
对任意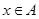 及
及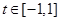 恒成立
恒成立
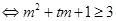 对任意
对任意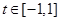 恒成立
恒成立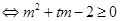 对任意
对任意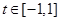 恒成立
恒成立
设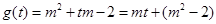 ,则问题又等价于
,则问题又等价于

即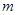 的取值范围是
的取值范围是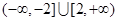 -----14分
-----14分
(1)a=1时,
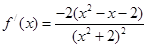 ,
, 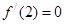 ,过点
,过点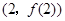 的切线方程为y=
的切线方程为y=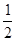 得到结论。
得到结论。(2)
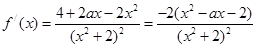 , ∵
, ∵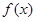 在区间
在区间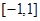 上是增函数,∴
上是增函数,∴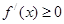 对
对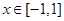 恒成立,即
恒成立,即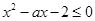 对
对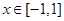 恒成立等价转化得到结论。
恒成立等价转化得到结论。(3)由
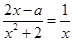 ,得
,得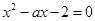 ,
,∵
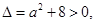 ∴
∴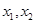 是方程
是方程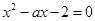 的两非零实根,
的两非零实根,∴
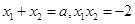 ,从而
,从而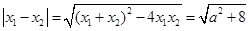
结合不等式得到结论。
解:(1)a=1时,
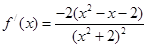 ,-------2分
,-------2分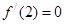 ,过点
,过点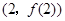 的切线方程为y=
的切线方程为y=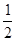 ----------4分
----------4分(2)
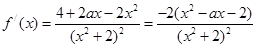 ,
,∵
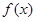 在区间
在区间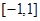 上是增函数,
上是增函数,∴
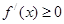 对
对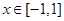 恒成立,
恒成立,即
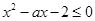 对
对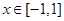 恒成立
恒成立 设
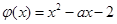 ,则问题等价于
,则问题等价于 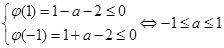 ,
, ∴
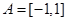 --------9
--------9(3)由
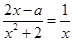 ,得
,得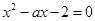 ,
,∵
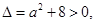 ∴
∴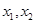 是方程
是方程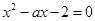 的两非零实根,
的两非零实根,∴
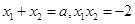 ,从而
,从而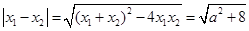 ,
,∵
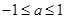 ,∴
,∴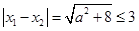 .
.∴不等式
 对任意
对任意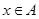 及
及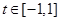 恒成立
恒成立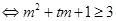 对任意
对任意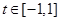 恒成立
恒成立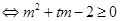 对任意
对任意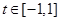 恒成立
恒成立设
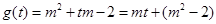 ,则问题又等价于
,则问题又等价于
即
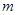 的取值范围是
的取值范围是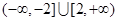 -----14分
-----14分
练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
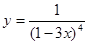 的导数.
的导数.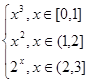 在区间[0,3]上的积分.
在区间[0,3]上的积分.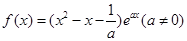 .
.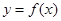 在点
在点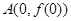 处的切线方程;
处的切线方程;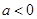 时,求函数
时,求函数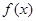 的单调区间.
的单调区间.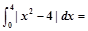 .
.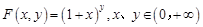 .
.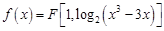 与直线
与直线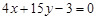 垂直的切线方程;
垂直的切线方程;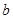 使曲线
使曲线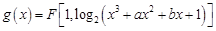 在
在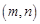 点处的切线斜率为
点处的切线斜率为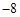 ,且
,且 ,求实数
,求实数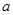 的取值范围.
的取值范围.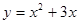 在点A(2,10)处的切线的斜率是
在点A(2,10)处的切线的斜率是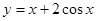 在区间
在区间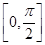 上的最大值是 .
上的最大值是 .  则
则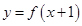 的单调减区间为( )
的单调减区间为( )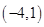
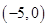
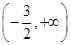
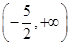
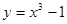 在x=1处的切线方程为 ( )
在x=1处的切线方程为 ( )