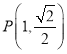题目内容
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,且将全班25人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
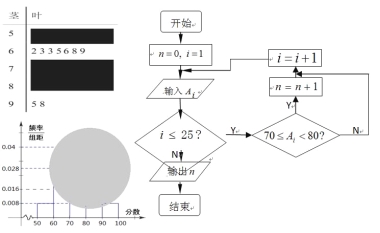
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
【答案】(Ⅰ)2,10,4(Ⅱ)众数75. 中位数73.5
【解析】
试题分析:(Ⅰ)由已知条件可知[50,60)之间的频率和频数可求得样本容易,结合频率分布直方图可得到各组频数;(Ⅱ)众数为出现次数最多的数,中位数为频率分布直方图中频率为0.5位置的数
试题解析:(Ⅰ)由直方图知:在[50,60)之间的频率为0.00810=0.08,
![]() 在[50,60)之间的频数为2;
在[50,60)之间的频数为2;
由程序框图知:在[70,80)之间的频数为10
所以分数在[80,90)之间的频数为25-2-7-10-2=4;
(Ⅱ)分数在[50,60)之间的频率为2/25=0.08;
分数在[60,70)之间的频率为7/25=0.28;
分数在[70,80)之间的频率为10/25=0.40;
分数在[80,90)之间的频率为4/25=0.16;
分数在[90,100]之间的频率为2/25=0.08;
估计该班的测试成绩的众数75. .....10分
设中位数为![]() ,则
,则![]() 得
得![]()

【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行![]() 天试销,每种单价试销
天试销,每种单价试销![]() 天,得到如下数据:
天,得到如下数据:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是![]() 元,
元,
为了获得最大利润,该单元卷的单价应定为多少元?
附:  ,
, ![]()
【题目】某初级中学有三个年级,各年级男、女生人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 | z | 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求z的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,将该样本看成一个总体,从中任选2名学生,求至少有1名女生的概率;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2, 1.5, 1.2, 1.5, 1.5, 1.3, 1.0, 1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.