题目内容
3.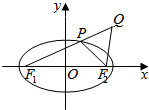 已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.
已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.(Ⅰ)设x为点P的横坐标,证明|$\overrightarrow{{F}_{1}P}$|=5+$\frac{4}{5}$x;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=9,求∠F1MF2的正切值;若不存在,请说明理由.
分析 (Ⅰ)设点P的坐标为(x,y),利用椭圆定义计算即得结论;
(Ⅱ)设点T(x,y),分$|\overrightarrow{PT}|=0$、|$\overrightarrow{PT}|≠0且|\overrightarrow{T{F_2}}|≠0$两种情况,结合向量数量积计算即可;
(Ⅲ)设在C上存在点M(x0,y0),易知S=9?$\left\{\begin{array}{l}{{{x}_{0}}^{2}+{{y}_{0}}^{2}=25}\\{4|{y}_{0}|=9}\end{array}\right.$,显然存在点M,使S=9,利用|$\overrightarrow{M{F}_{1}}$|•|$\overrightarrow{M{F}_{2}}$|cos∠F1MF2=9=$\frac{1}{2}$|$\overrightarrow{M{F}_{1}}$|•|$\overrightarrow{M{F}_{2}}$|sin∠F1MF2,计算即可.
解答 (Ⅰ)证明:设点P的坐标为(x,y).
记$|\overrightarrow{{F_1}P}|={r_1},|\overrightarrow{{F_2}P}|={r_2}$,
则${r_1}=\sqrt{{{(x+4)}^2}+{y^2}},{r_2}=\sqrt{{{(x-4)}^2}+{y^2}}$.
由${r_1}+{r_2}=10,r_1^2-r_2^2=16x,得|\overrightarrow{{F_1}P}|={r_1}=5+\frac{4}{5}x$;
(Ⅱ)解:设点T的坐标为(x,y).
当$|\overrightarrow{PT}|=0$时,点(5,0)和点(-5,0)在轨迹上.
当|$\overrightarrow{PT}|≠0且|\overrightarrow{T{F_2}}|≠0$时,由$\overrightarrow{PT}•\overrightarrow{T{F_2}}=0$,得$\overrightarrow{PT}⊥\overrightarrow{T{F_2}}$.
又$|\overrightarrow{PQ}|=|\overrightarrow{P{F_2}}|$,所以T为线段F2Q的中点.
在△QF1F2中,$|\overrightarrow{OT}|=\frac{1}{2}|\overrightarrow{{F_1}Q}|=5$,所以有x2+y2=25.
综上所述,点T的轨迹C的方程是x2+y2=25;
(Ⅲ)结论:在点T的轨迹C上,存在点M使△F1MF2的面积S=9,此时∠F1MF2的正切值为2.
理由如下:
C上存在点M(x0,y0)使S=9的充要条件是$\left\{\begin{array}{l}{{{x}_{0}}^{2}+{{y}_{0}}^{2}=25}\\{4|{y}_{0}|=9}\end{array}\right.$,
显然|y0|=$\frac{9}{4}$<5,∴存在点M,使S=9;
不妨取y0=$\frac{9}{4}$,则$\overrightarrow{M{F}_{1}}$=(-4-x0,-$\frac{9}{4}$),$\overrightarrow{M{F}_{2}}$=(4-x0,-$\frac{9}{4}$),
∵$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}=|\overrightarrow{M{F_1}}|•|\overrightarrow{M{F_2}}|cos∠{F_1}M{F_2}$
=(-4-x0,-$\frac{9}{4}$)•(4-x0,-$\frac{9}{4}$)
=x02-16+($\frac{9}{4}$)2
=x02+($\frac{9}{4}$)2-16
=25-16=9,
又∵S=$\frac{1}{2}$|$\overrightarrow{M{F}_{1}}$|•|$\overrightarrow{M{F}_{2}}$|sin∠F1MF2=9,
∴|$\overrightarrow{M{F}_{1}}$|•|$\overrightarrow{M{F}_{2}}$|cos∠F1MF2=$\frac{1}{2}$|$\overrightarrow{M{F}_{1}}$|•|$\overrightarrow{M{F}_{2}}$|sin∠F1MF2,
∴tan∠F1MF2=2.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于难题.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
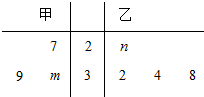 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式${(\frac{x}{m}+\frac{n}{x})^4}$展开式中的常数项为$\frac{128}{3}$.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式${(\frac{x}{m}+\frac{n}{x})^4}$展开式中的常数项为$\frac{128}{3}$.
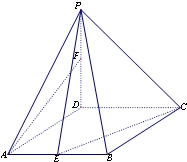 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.