题目内容
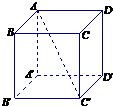
在棱长为1的正方体ABCD-A′B′C′D′中,若点P是棱上一点,则满足|PA|+|PC′|=2的点P的个数为( )
| A.4 | B.6 | C.8 | D.12 |

∵正方体的棱长为1
∴AC′=
∵|PA|+|PC'|=2
∴点P是以2c=
为焦距,以a=1为长半轴,以
为短半轴的椭圆
∵P在正方体的棱上
∴P应是椭圆与正方体与棱的交点
结合正方体的性质可知,满足条件的点应该在棱B'C',C'D',CC',AA',AB,AD上各有一点满足条件
故选B
∴AC′=
| 3 |
∵|PA|+|PC'|=2
∴点P是以2c=
| 3 |
| 1 |
| 2 |
∵P在正方体的棱上
∴P应是椭圆与正方体与棱的交点
结合正方体的性质可知,满足条件的点应该在棱B'C',C'D',CC',AA',AB,AD上各有一点满足条件
故选B

练习册系列答案
相关题目
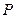 是椭圆
是椭圆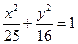 上的一点,
上的一点,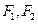 是焦点,若
是焦点,若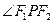 是直角,则
是直角,则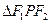 的面积为 。
的面积为 。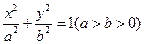 与直线
与直线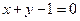 相交于
相交于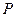 、
、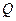 两点,且
两点,且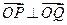 (
(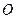 为坐标原点).(Ⅰ)求证:
为坐标原点).(Ⅰ)求证: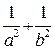 等于定值;
等于定值;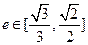 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围.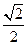
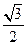
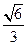
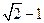
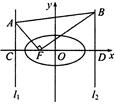
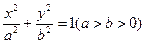 的左、右准线分别为
的左、右准线分别为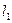 、
、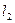 ,且分别交
,且分别交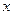 轴于
轴于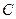 、
、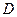 两点,从
两点,从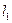 上一点
上一点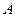 发出一条光线经过椭圆的左焦点
发出一条光线经过椭圆的左焦点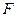 被
被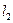 交于点
交于点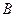 ,若
,若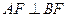 ,且
,且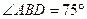 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )