题目内容
求经过点(2,-3)且与椭圆9x2+4y2=36有共同焦点的椭圆方程.
把9x2+4y2=36转化为标准方程,
得
+
=1,
∵c=
=
,
∴其焦点坐标为F1(0,-
),F2(0,
),
∵所求椭圆的焦点坐标为F1(0,-
),F2(0,
),
∴设所求椭圆方程为
+
=1,
把(2,-3)代入,得
+
=1,
解得a2=15,或a2=3(舍)
∴所求的椭圆方程为
+
=1.
得
| x2 |
| 4 |
| y2 |
| 9 |
∵c=
| 9-4 |
| 5 |
∴其焦点坐标为F1(0,-
| 5 |
| 5 |
∵所求椭圆的焦点坐标为F1(0,-
| 5 |
| 5 |
∴设所求椭圆方程为
| x2 |
| a2-5 |
| y2 |
| a2 |
把(2,-3)代入,得
| 4 |
| a2-5 |
| 9 |
| a2 |
解得a2=15,或a2=3(舍)
∴所求的椭圆方程为
| x2 |
| 10 |
| y2 |
| 15 |

练习册系列答案
相关题目
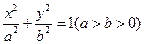 与直线
与直线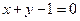 相交于
相交于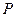 、
、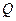 两点,且
两点,且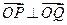 (
(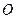 为坐标原点).(Ⅰ)求证:
为坐标原点).(Ⅰ)求证: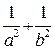 等于定值;
等于定值;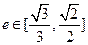 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围.