题目内容
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率
,离心率![]() ,其右焦点为
,其右焦点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作夹角为
作夹角为![]() 的两条直线
的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 和
和![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)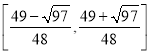 .
.
【解析】
(1)由已知短轴长求出![]() ,离心率求出
,离心率求出![]() 关系,结合
关系,结合![]() ,即可求解;
,即可求解;
(2)当直线![]() 的斜率都存在时,不妨设直线
的斜率都存在时,不妨设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与椭圆方程联立,利用相交弦长公式求出
与椭圆方程联立,利用相交弦长公式求出![]() ,
,![]() 斜率为
斜率为![]() ,求出
,求出![]() ,得到
,得到![]() 关于
关于![]() 的表达式,根据表达式的特点用“
的表达式,根据表达式的特点用“![]() ”判别式法求出
”判别式法求出![]() 范围,当
范围,当![]() 有一斜率不存在时,另一条斜率为
有一斜率不存在时,另一条斜率为![]() ,根据弦长公式,求出
,根据弦长公式,求出![]() ,即可求出结论.
,即可求出结论.
(1)由![]() 得
得![]() ,又由
,又由![]() 得
得![]() ,
,
则![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(2)由(1)知![]() ,
,
①当直线![]() 的斜率都存在时,
的斜率都存在时,
由对称性不妨设直线![]() 的方程为
的方程为![]() ,
,
由![]() ,
,
![]() ,设
,设![]() ,
,
则![]() ,
,
则![]() ,
,
由椭圆对称性可设直线![]() 的斜率为
的斜率为![]() ,
,
则 ,
,
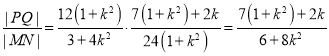
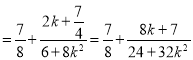 .
.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,由
时,由![]() 得
得![]() ,所以
,所以![]() ,
,
即![]() ,且
,且![]() .
.
②当直线![]() 的斜率其中一条不存在时,
的斜率其中一条不存在时,
根据对称性不妨设设直线![]() 的方程为
的方程为![]() ,
,![]() 斜率不存在,
斜率不存在,
则![]() ,
,![]() ,
,
此时 .
.
若设![]() 的方程为
的方程为![]() ,
,![]() 斜率不存在,
斜率不存在,
则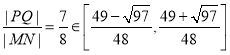 ,
,
综上可知![]() 的取值范围是
的取值范围是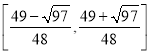 .
.

练习册系列答案
相关题目
【题目】
|
某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
P(A);
(Ⅱ)求![]() 的分布列及期望
的分布列及期望![]()