题目内容
【题目】已知![]() 是等差数列,其前
是等差数列,其前![]() 项中的奇数项的和与偶数项的和之差为
项中的奇数项的和与偶数项的和之差为![]() .
.
(1)请证明这一结论对任意等差数列![]() (
(![]() 中各项均不为零)恒成立;
中各项均不为零)恒成立;
(2)请类比等差数列的结论,对于各项均为正数的等比数列![]() ,提出猜想,并加以证明.
,提出猜想,并加以证明.
【答案】(1)证明见解析(2)类比猜想:各项均为正数的等比数列![]() 的前
的前![]() 项中奇数项的积与偶数项的积的比为
项中奇数项的积与偶数项的积的比为![]() ,证明见解析
,证明见解析
【解析】
(1)由![]() ,
,![]() 可得
可得![]()
(2)类比猜想可得:各项均为正数的等比数列![]() 的前
的前![]() 项中奇数项的积与偶数项的积的比为
项中奇数项的积与偶数项的积的比为![]() ,然后证明出来即可.
,然后证明出来即可.
证明:(1)记![]() 为等差数列
为等差数列![]() 前
前![]() 项中奇数项的和,
项中奇数项的和,
![]() 为等差数列
为等差数列![]() 前
前![]() 项中偶数项的和,
项中偶数项的和,
由等差数列的前![]() 项和公式可得
项和公式可得![]() ,
,
![]() ,
,
![]() .
.
![]() 命题成立.
命题成立.
(2)解:类比猜想可得:各项均为正数的等比数列![]() 的前
的前![]() 项中奇数项的积与偶数项的积的比为
项中奇数项的积与偶数项的积的比为![]() .
.
证明:记各项均为正数的等比数列![]() 的前
的前![]() 项中奇数项的积为
项中奇数项的积为![]() ,
,
偶数项的积为![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,
,
 ,即
,即![]() .
.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】某省积极响应教育部号召实行新课程改革,为了调查某校高三学生的物理考试成绩是否达到![]() 级与学生性别是否有关,从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表:
级与学生性别是否有关,从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表:
考试成绩达到 | 考试成绩未达到 | 总计 | |
男生 | 26 | 40 | |
女生 | 6 | ||
总计 | 70 |
(1)(ⅰ)将![]() 列联表补充完整;
列联表补充完整;
(ⅱ)据此列联表判断,能否有![]() 的把握认为“物理考试成绩是否达到级与性别有关”?
的把握认为“物理考试成绩是否达到级与性别有关”?
(2)将频率视作概率,从该校高三年级任意抽取3名学生的成绩,求物理考试成绩达到![]() 级的人数的分布列及期望.
级的人数的分布列及期望.
附: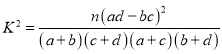
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10..828 |
【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查![]() 结果只有“满意”和“不满意”两种
结果只有“满意”和“不满意”两种![]() ,从被调查的学生中随机抽取了50人,具体的调查结果如表:
,从被调查的学生中随机抽取了50人,具体的调查结果如表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 5 | 9 | 11 | 9 | 7 | 9 |
满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
