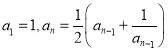题目内容
【题目】如图所示,我国某海岸线可看作由圆弧AB和射线BC连接而成,其中圆弧AB所在圆O的半径为12海里,圆心角为120°,规定外轮除特许外,不得进入离我国海岸线12海里以内的区域.在港口A处设有观察站,外轮一旦进入规定区域,观察站会接收到预警信号,现从A处测得一外轮在北偏东60°,距离港口x海里的P处,沿直线PA方向航行.
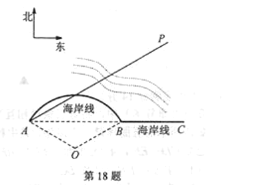
(1)当x=30时,分别求出外轮到海岸线BC和弧AB的最短距离,并判断观察站是否接收到预警信号?
(2)当x为何值时,观察站开始接收到预警信号?
【答案】(1)最短距离为6![]() 12,不能接收到预警信号;(2)6+6
12,不能接收到预警信号;(2)6+6![]()
【解析】
(1)根据已知条件求出点![]() 到射线
到射线![]() 的距离,和到圆弧
的距离,和到圆弧![]() 的最小值,再与12海里进行比较即可得判断;
的最小值,再与12海里进行比较即可得判断;
(2)由(1)知 ![]() 到弧
到弧![]() 的距离比
的距离比![]() 到射线
到射线![]() 的距离小,所以只要列出点
的距离小,所以只要列出点![]() 到圆弧
到圆弧![]() 的最小值为
的最小值为![]() 的关系式即可求
的关系式即可求![]() 的值.
的值.
(1)以![]() 为坐标原点,建立如图所示的直角坐标系,
为坐标原点,建立如图所示的直角坐标系,

当![]() 时,由直角三角形中
时,由直角三角形中![]() ,可得
,可得![]() 到
到![]() 的距离为
的距离为![]() ,
,
此时![]() 即
即![]() ,可得P到弧
,可得P到弧![]() 的最短距离为
的最短距离为
![]() ,可得判断观察站不能接收到预警信号;
,可得判断观察站不能接收到预警信号;
(2)当![]() 到弧
到弧![]() 的距离为
的距离为![]() ,由于
,由于![]() 到
到![]() 的距离大于
的距离大于![]() ,
,
设![]() ,可得
,可得 ,且
,且![]() ,
,
可得![]() ,即有
,即有![]() ,
,
解得![]() (负的舍去),
(负的舍去),
当![]() 为
为![]() 海里时,观察站开始接收到预警信号.
海里时,观察站开始接收到预警信号.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目