题目内容
【题目】已知点
是抛物线
上一点，
为
的焦点．
（1）若
，
是上的两点，证明：
，
，
依次成等比数列.
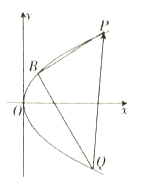
（2）过
作两条互相垂直的直线与的另一个交点分别交于
，
(在的上方），求向量
在
轴正方向上的投影的取值范围.
【答案】（1）详见解析；（2）
.
【解析】
（1）由在抛物线上求P,再利用焦半径公式求
，
，
，再利用等比数列定义证明即可（2）设直线
的方程为
，与
联立，得
，由
，求k的范围，并求得P坐标，同理求得Q坐标，则向量
在
轴正方向上的投影为
，求函数
的范围即求得结果
（1）证明：
在抛物线
上，
，
.
，
，
，
，，依次成等比数列.
(2)设直线的方程为，与联立，得
则 
，
，
设 
，
，则
，即
在
的上方
，则
.
以
代
，得
，
则向量在轴正方向上的投影为，
设函数，则
在
上单调递减，在
上单调递增，从而
，
故向量在轴正方向上的投影的取值范围为
.
练习册系列答案
名校课堂系列答案
相关题目
