题目内容
【题目】已知定义在R上的奇函数f（x），当x∈（0，+∞）时的解析式为f（x）=﹣x2+4x﹣3．
（1）求这个函数在R上的解析式；
（2）作出f（x）的图象，并根据图象直接写出函数f（x）的单调区间． 
【答案】
（1）解：当x＜0时，﹣x＞0，∵f（x）为R上的奇函数，∴f（﹣x）=﹣f（x），
∴f（x）=﹣f（﹣x）=﹣[﹣（﹣x）2+4（﹣x）﹣3]=x2+4x+3，
即x＜0时，f（x）=x2+4x+3．
当x=0时，由f（﹣x）=﹣f（x）得：f（0）=0，
所以，f（x）=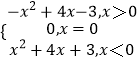 
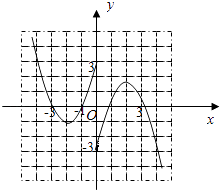
（2）解：作出f（x）的图象（如图所示）
数形结合可得函数f（x）的减区间：
（﹣∞，﹣2）、（2，+∞）；增区间为[﹣2，0）、（0，2]．
【解析】（1）根据当x∈（0，+∞）时的解析式，利用奇函数的性质，求得x≤0时函数的解析式，从而得到函数在R上的解析式．（2）根据函数的解析式、奇函数的性质，作出函数的图象，数形结合可得函数f（x）的单调区间．
练习册系列答案
智慧小复习系列答案
相关题目
