题目内容
【题目】如图所示,已知抛物线C1:x2=2py的焦点在抛物线C2:![]() ,点P是抛物线C1上的动点.
,点P是抛物线C1上的动点.

(1)求抛物线C1的方程及其准线方程;
(2)过点P作抛物线C2的两条切线,M,N分别为两个切点,设点P到直线MN的距离为d,求d的最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)由题意抛物线C1的焦点为抛物线C2的顶点(0,1),由此算出p=2,从而得到抛物线C1的方程,得到C1的准线方程;(2)设P(2t,t2),用直线方程的点斜式列出直线PM方程并将点P坐标代入,化简可得![]() 同理得到
同理得到![]() .然后利用一元二次方程根与系数的关系,算出x1+x2=4t,x1x2=2t2﹣2,将直线MN的两点式方程化简并代入前面算出的式可得MN的方程为y=2tx+2﹣t2.最后利用点到直线的距离公式列式,采用换元法并且运用基本不等式求最值,即可算出P到直线MN的距离d的最小值为
.然后利用一元二次方程根与系数的关系,算出x1+x2=4t,x1x2=2t2﹣2,将直线MN的两点式方程化简并代入前面算出的式可得MN的方程为y=2tx+2﹣t2.最后利用点到直线的距离公式列式,采用换元法并且运用基本不等式求最值,即可算出P到直线MN的距离d的最小值为![]() .
.
(1)C1的焦点为![]() ,所以
,所以![]() =0+1,得p=2.故C1的方程为x2=4y,其准线方程为y=-1.
=0+1,得p=2.故C1的方程为x2=4y,其准线方程为y=-1.
(2)设P(2t,t2),M![]() ,N
,N![]() ,则PM的方程为y-
,则PM的方程为y-![]() =x1(x-x1),将P点坐标代入得t2=2tx1-
=x1(x-x1),将P点坐标代入得t2=2tx1-![]() x+1,即x-4tx1+2t2-2=0,同理得x-4tx2+2t2-2=0.MN的方程为y-
x+1,即x-4tx1+2t2-2=0,同理得x-4tx2+2t2-2=0.MN的方程为y-![]() =
=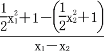 (x-x1),即y-
(x-x1),即y-![]() =
=![]() (x1+x2)(x-x1).
(x1+x2)(x-x1).
由![]() 得x1+x2=4t,
得x1+x2=4t,![]() x-2tx1=1-t2,所以直线MN的方程为y=2tx+2-t2.
x-2tx1=1-t2,所以直线MN的方程为y=2tx+2-t2.
于是d=![]() =2
=2![]() .
.
令s=1+4t2(s≥1),则d=![]()
![]() ≥
≥![]()
![]() =
=![]() (当且仅当s=3时取等号),
(当且仅当s=3时取等号),
所以d的最小值为![]() .
.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目


