��Ŀ����
����Ŀ��ij�������ȡ������ҵ�������Ͻ�˰�����{��λ��Ԫ�����������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�������Ͻ�˰�շ�Χ��[0��100]�������ݷ���Ϊ[0��20����[20��40��[40��60��[60��80����[80��100��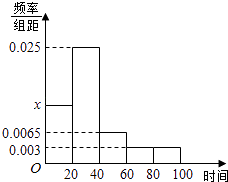
��1����ֱ��ͼ��x��ֵ��
��2��������Ͻ�˰�ղ�����60��Ԫ����ҵ�����������Żݣ�������ȡ��ҵ1200�����Թ����ж�����ҵ�������������Żݣ�
��3������ҵ����ѡ4������4����ҵ���Ͻ�˰������20��Ԫ�ĸ�����ΪX����X�ķֲ��к���ѧ��������ֱ��ͼ�е�Ƶ����Ϊ���ʣ�
���𰸡�
��1���⣺��Ƶ�ʷֲ�ֱ��ͼ�ã�
��x+0.025+0.0065+0.003+0.003����20=1��
���x=0.0125��
��2����Ƶ�ʷֲ�ֱ��ͼ�����Ͻ�˰�ղ�����60��Ԫ����ҵ��ռƵ��Ϊ��0.003+0.003����20=0.12��
�����Ͻ�˰�ղ�����60��Ԫ����ҵ�����������Żݣ�����ȡ��ҵ1200����
������У�1200��0.12=144����ҵ�������������Żݣ�
��3����ҵ���Ͻ�˰������20��Ԫ��Ƶ��p=0.0125��20=0.25��
����ҵ����ѡ4������4����ҵ���Ͻ�˰������20��Ԫ�ĸ�����ΪX��
��X��B��4�� ![]() ����
����
P��X=0��= ![]() =
= ![]() ��
��
P��X=1��= ![]() =
= ![]() ��
��
P��X=2��= ![]() =
= ![]() ��
��
P��X=3��= ![]() =
= ![]() ��
��
P��X=4��= ![]() =
= ![]() ��
��
��X�ķֲ���Ϊ��
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
E��X��= ![]() =1��
=1��
����������1����Ƶ��ֱ��ͼ�������Ϊ1�ɵ�x��ֵ����2����Ƶ�ʷֲ�ֱ��ͼ��������Ͻ�˰�ղ�����60��Ԫ����ҵ��ռƵ��Ϊ0.12���ɹ��Ƴ���144����ҵ���������Żݣ���3����ҵ���Ͻ�˰������20��Ԫ��Ƶ��Ϊ0.25����ѡ�ĸ���ҵ���Ͻ�˰������20��Ԫ����ȡֵΪ0��1,2,3,4��������ʣ��г��ֲ��У�������� .

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�����Ŀ��ij�Ƽ���˾����һ���ֻ�����оƬ��������������ָ�껮��Ϊ��ָ����ڻ����70Ϊ�ϸ�Ʒ��С��70Ϊ��Ʒ���������ȡ����оƬ��120�����м�⣬�����ͳ�������
����ָ�� | [50��60�� | [60��70�� | [70��80�� | [80��90�� | [90��100] |
оƬ���������� | 8 | 22 | 45 | 37 | 8 |
��֪����һ��оƬ�����Ǻϸ�Ʒ��ӯ��400Ԫ�����Ǵ�Ʒ�����50Ԫ��
�����Թ�������һ��оƬΪ�ϸ�Ʒ�ĸ��ʣ���������3��оƬ����õ���������700Ԫ�ĸ��ʣ�
���Ǧ�Ϊ����4��оƬ���õ�����������������εķֲ��к���ѧ������