Question

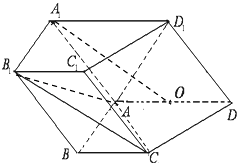
【题目】平面上，点A、C为射线PM上的两点，点B、D为射线PN上的两点，则有 （其中S△PAB、S△PCD分别为△PAB、△PCD的面积）；空间中，点A、C为射线PM上的两点，点B、D为射线PN上的两点，点E、F为射线PL上的两点，则有 =（其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积）．

Answer 1

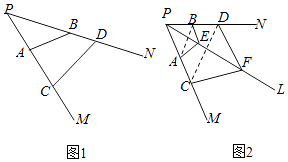
【答案】
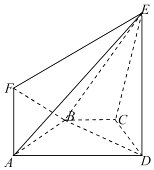
【解析】解：设PM与平面PDF所成的角为α，

则A到平面PDF的距离h1=PAsinα，C到平面PDF的距离h2=PCsinα，

∴VP﹣ABE=VA﹣PBE= = ，

VP﹣CDF=VC﹣PDF= = ，

∴ = ．

故答案为： ．

设PM与面PDF所成的角为α，则两棱锥的高的比为,底面积比为,根据棱锥的体积公式即可得出体积比.