题目内容
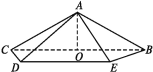
【题目】如图,ABCD是边长为a的正方形,PA⊥平面ABCD.

(1)若PA=AB,点E是PC的中点,求直线AE与平面PCD所成角的正弦值;
(2)若BE⊥PC且交点为E,BE=![]() a,G为CD的中点,线段AB上是否存在点F,使得EF∥平面PAG?若存在,求AF的长;若不存在,请说明理由.
a,G为CD的中点,线段AB上是否存在点F,使得EF∥平面PAG?若存在,求AF的长;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)以A为坐标原点建立坐标系,得出![]() 以及平面PCD的一个法向量,设直线AE与平面PCD所成角为
以及平面PCD的一个法向量,设直线AE与平面PCD所成角为![]() ,由sin
,由sin![]() =|cos<
=|cos<![]() ,m>|,即可求出直线AE与平面PCD所成角的正弦值。
,m>|,即可求出直线AE与平面PCD所成角的正弦值。
(2)设P(0,0,c)(c>0),![]() =λ
=λ![]() 由BE=
由BE=![]() a以及BE⊥PC可得λ=
a以及BE⊥PC可得λ=![]() ,c=a设AF=l,求出平面PAG的法向量为n,由
,c=a设AF=l,求出平面PAG的法向量为n,由![]() ·n=0即可得出答案。
·n=0即可得出答案。
(1)以A为原点,建立如图所示的坐标系,则A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),P(0,0,a),E![]() =(a,0,0),
=(a,0,0),![]() =(0,a,-a).
=(0,a,-a).
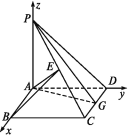
设平面PCD的法向量m=(x,y,z),则![]()
取m=(0,1,1),
则cos<![]() ,m>=
,m>=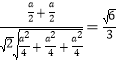 .
.
设直线AE与平面PCD所成角为![]() ,
,
则sin![]() =|cos<
=|cos<![]() ,m>|,所以直线AE与平面PCD所成角的正弦值为
,m>|,所以直线AE与平面PCD所成角的正弦值为![]() .
.
(2)G![]() ,设P(0,0,c)(c>0),
,设P(0,0,c)(c>0),
则![]() =(-a,-a,c).
=(-a,-a,c).
设![]() =λ
=λ![]() ,则E((1-λ)a,(1-λ)a,λc),
,则E((1-λ)a,(1-λ)a,λc),
∴![]() =(-λa,(1-λ)a,λc).
=(-λa,(1-λ)a,λc).
∵BE=![]() a,
a,
∴(-λa)2+[(1-λ)a]2+(λc)2=![]() . ①
. ①
∵BE⊥PC,∴λa2-(1-λ)a2+λc2=0.
∴c2=![]() =a2. ②
=a2. ②
由①②解得λ=![]() ,c=a,
,c=a,
∴E![]() ,P(0,0,a).
,P(0,0,a).
若存在满足条件的点F,可设AF=l(0≤l≤a),
则F(l,0,0),![]() .
.
设平面PAG的法向量为n=(s,t,p),
则 ∴n=(-2,1,0).
∴n=(-2,1,0).
∵EF∥平面PAG,∴![]() ·n=0.
·n=0.
∴-2l+![]() a-
a-![]() a=0,∴l=
a=0,∴l=![]() a.
a.
∴存在满足条件的点F,且AF=![]() a.
a.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案