题目内容
9．
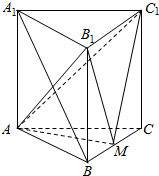如图，直三棱柱ABC-A1B1C1的底面是边长为A的正三角形，点M在边BC上，△AMC1是以M为直角顶点的等腰直角三角形．（1）求证：直线A1B∥平面AMC1；
（2）求三棱锥C1-AB1M的高．
分析 （1）根据等腰直角三角形，可得AM⊥C1M且AM=C1M，根据三垂线定理可知AM⊥CM，而底面ABC为边长为a的正三角形，证得点M为BC边的中点，连接A1C，交AC1于点N，连接MN，则N为A1C的中点，可得MN∥A1B，即可证明直线A1B∥平面AMC1；
（2）利用${V}_{{C}_{1}-A{B}_{1}M}$=${V}_{A-{B}_{1}M{C}_{1}}$，求三棱锥C1-AB1M的高．
解答 （1）证明：∵△AMC1为以点M为直角顶点的等腰直角三角形，
∴AM⊥C1M且AM=C1M
∵三棱柱ABC-A1B1C1，∴CC1⊥底面ABC
∴C1M在底面内射影为CM，AM⊥CM．
∵底面ABC为边长为a的正三角形，
∴点M为BC边的中点
连接A1C，交AC1于点N，连接MN，则N为A1C的中点
∴MN∥A1B，
∵MN?平面AMC1，A1B?平面AMC1，∴A1B∥平面AMC1；
（2）解：设三棱锥C1-AB1M的高为h，
∵AM⊥平面B1BCC1，∴${V}_{{C}_{1}-A{B}_{1}M}$=${V}_{A-{B}_{1}M{C}_{1}}$，
∴$\frac{1}{3}•\frac{3}{8}{a}^{2}h=\frac{1}{3}•\frac{\sqrt{2}}{4}{a}^{2}•\frac{\sqrt{3}}{2}a$，∴h=$\frac{\sqrt{6}}{3}$a．．
点评 本题主要考查了点线的位置关系，以及点到平面的距离的计算，同时考查了空间想象能力和计算能力，以及转化与划归的思想，属于中档题．
练习册系列答案
相关题目
4．已知角α终边与单位圆x2+y2=1的交点为$P（\frac{1}{2}，y）$，则$sin（\frac{π}{2}+2α）$=（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | 1 |
1．函数f（x）=sin（-2x）的一个递增区间是（ ）
| A． | $（0，\frac{π}{4}）$ | B． | $（-π，-\frac{π}{2}）$ | C． | $（\frac{3π}{4}，2π）$ | D． | $（-\frac{π}{2}，-\frac{π}{4}）$ |
18．三棱锥P-ABC中，已知∠APC=∠BPC=∠APB=$\frac{π}{3}$，点M是△ABC的重心，且$\overrightarrow{PA}$•$\overrightarrow{PB}$+$\overrightarrow{PB}$$•\overrightarrow{PC}$+$\overrightarrow{PC}$$•\overrightarrow{PA}$=9，则|$\overrightarrow{PM}$|的最小值为（ ）
| A． | 2$\sqrt{2}$ | B． | $\sqrt{6}$ | C． | $\frac{4\sqrt{3}}{3}$ | D． | 2 |
19．已知f（x）是定义在R上的奇函数，f（-1）=-1，且当x＞0时，有xf′（x）＞f（x），则不等式f（x）＞x的解集是（ ）
| A． | （-1，0） | B． | （1，+∞） | C． | （-1，0）∪（1，+∞） | D． | （-∞，-1）∪（1，+∞） |