题目内容
1.函数f(x)=sin(-2x)的一个递增区间是( )| A. | $(0,\frac{π}{4})$ | B. | $(-π,-\frac{π}{2})$ | C. | $(\frac{3π}{4},2π)$ | D. | $(-\frac{π}{2},-\frac{π}{4})$ |
分析 利用诱导公式变形,然后求函数y=sin2x的减区间得答案.
解答 解:f(x)=sin(-2x)=-sin(2x),
由2kπ+$\frac{π}{2}$≤2x≤2kπ+$\frac{3π}{2}$,
得kπ+$\frac{π}{4}$≤x≤kπ+$\frac{3π}{4}$,
取k=-1,得函数f(x)=sin(-2x)的一个递增区间是$(-\frac{3π}{4},-\frac{π}{4})$,
而$(-\frac{π}{2},-\frac{π}{4})$?$(-\frac{3π}{4},-\frac{π}{4})$.
故选:D.
点评 本题考查与三角函数有关的复合函数单调性的求法,复合函数的单调性满足“同增异减”的原则,是基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13.已知函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x},}&{0<x≤3}\\{-\frac{2}{3}x+\frac{16}{3},}&{x>3}\end{array}\right.$,若函数g(x)=f(x)-m有三个互不相等的零点a、b、c,则abc的取值范围为( )
| A. | (2,$\frac{10}{3}$) | B. | (0,5) | C. | (6,10) | D. | (3,5) |
11.已知集合A={x∈N|x-3≤0},B=f{x∈Z|x2+x-2≤0},则集合A∩B=( )
| A. | {1} | B. | {0,1} | C. | {0,1,2} | D. | {1,2} |
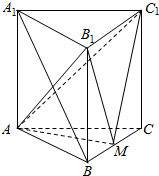 如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形. 为了调查高一新生中女生的体重情况,校卫生室随机选取20名女生作为样本测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(55,60]上的女生数之比为4:3.
为了调查高一新生中女生的体重情况,校卫生室随机选取20名女生作为样本测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(55,60]上的女生数之比为4:3.