题目内容
4.已知角α终边与单位圆x2+y2=1的交点为$P(\frac{1}{2},y)$,则$sin(\frac{π}{2}+2α)$=( )| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 1 |
分析 由条件利用任意角的三角函数的定义,求得cosα的值,再利用诱导公式、二倍角的余弦公式求得$sin(\frac{π}{2}+2α)$的值.
解答 解:由题意可得,cosα=$\frac{1}{2}$,
则$sin(\frac{π}{2}+2α)$=cos2α=2cos2α-1=2×$\frac{1}{4}$-1=-$\frac{1}{2}$,
故选:A.
点评 本题主要考查任意角的三角函数的定义,诱导公式、二倍角的余弦公式的应用,属于基础题.

练习册系列答案
相关题目
14.下列说法中正确的是( )
| A. | 若命题p:?x∈R有x2>0,则¬p:?x∈R有x2≤0 | |
| B. | 若p是q的充分不必要条件,则¬p是¬q的必要不充分条件 | |
| C. | 若命题p:$\frac{1}{x-1}$>0,则¬p:$\frac{1}{x-1}$≤0 | |
| D. | 方程ax2+x+a=0有唯一解的充要条件是a=±$\frac{1}{2}$ |
15.实数X,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+3y-3≥0\\ 3x+y-9≤0\end{array}\right.$,若z=ax+y的最大值为2a+3,则a的取值范围是( )
| A. | [-3,1] | B. | [-1,3] | C. | (-∞,1] | D. | [3,+∞) |
13.已知函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x},}&{0<x≤3}\\{-\frac{2}{3}x+\frac{16}{3},}&{x>3}\end{array}\right.$,若函数g(x)=f(x)-m有三个互不相等的零点a、b、c,则abc的取值范围为( )
| A. | (2,$\frac{10}{3}$) | B. | (0,5) | C. | (6,10) | D. | (3,5) |
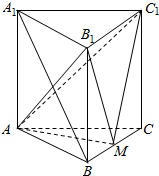 如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形.