题目内容

19．要分配甲、乙、丙、丁、戊5名同学去参加三项不同的教学活动，其中活动一和活动二各要2人，活动三要1人，每人只能参加一项活动，且甲，乙两人不能参加同一活动，则一共有24_种不同的分配方法．

分析 间接法：先求出活动一和活动二各要2人，活动共有三要1人的方法种数，去掉甲，乙两人参加同一活的方法种数即可．

解答 解：由题意把甲、乙、丙、丁、戊5人分配去参加三项不同的活动，
其中活动一和活动二各要2人，活动三要1人共有${C}_{5}^{2}•{C}_{3}^{2}$=30种方法，
其中甲，乙两人参加同一活动${C}_{3}^{2}$+${C}_{3}^{2}$=6种方法，
故符合题意得方法共30-6=24种，
故答案为：24．

点评 本题考查排列组合的应用，间接法是解决问题的关键，属中档题．

练习册系列答案
相关题目
9．在△ABC中，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，O为△ABC的重心，则$\overrightarrow{OA}$可用$\overrightarrow{a}$，$\overrightarrow{b}$表示为$-\frac{1}{3}$（$\overrightarrow{a}$+$\overrightarrow{b}$）．
10．已知i为虚数单位，若$\frac{1+i}{z}=1-2i$，则复数z所对应的点所在的象限是（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
7．一个平行四边形的三个顶点的坐标为（-1，2），（3，4），（4，-2），点（x，y）在这个平行四边形的内部或边上，则z=2x-5y的最大值与最小值的和等于（　　）
A．8B．6C．-12D．-24
14．下列说法中正确的是（　　）
A．若命题p：?x∈R有x2＞0，则￢p：?x∈R有x2≤0
B．若p是q的充分不必要条件，则￢p是￢q的必要不充分条件
C．若命题p：$\frac{1}{x-1}$＞0，则￢p：$\frac{1}{x-1}$≤0
D．方程ax2+x+a=0有唯一解的充要条件是a=±$\frac{1}{2}$
4．在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，BC=2AD=4，AB=CD=$\sqrt{10}$，∠DBC=45°
（1）证明：BD⊥平面PAC；
（2）若二面角A-PC-D的大小为60°，求四棱锥P-ABCD的体积．
11．已知向量$\overrightarrow{m}$=（2sinωx，cos2ωx-sin2ωx），$\overrightarrow{n}$=（$\sqrt{3}$cosωx，1）其中ω＞0，x∈R，若函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$的最小正周期为π．
（1）求ω的值及f（x）的对称轴方程；
（2）在△ABC中，角A，B，C的对边为a，b，c，若f（B）=-2，BC=$\sqrt{3}$，2bcosA=$\sqrt{3}$（ccosA+acosC），求$\overrightarrow{BA}$•$\overrightarrow{BC}$的值．
8．若不等式kx2-2x+1-k＜0对满足-2≤k≤2的所有k都成立，则x的取值范围是（$\frac{-1+\sqrt{7}}{2}$，$\frac{1+\sqrt{3}}{2}$）．
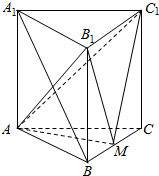9．如图，直三棱柱ABC-A1B1C1的底面是边长为A的正三角形，点M在边BC上，△AMC1是以M为直角顶点的等腰直角三角形．
（1）求证：直线A1B∥平面AMC1；
（2）求三棱锥C1-AB1M的高．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网