题目内容
如图,P是双曲线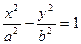 (
(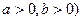 右支上的一点,
右支上的一点, ,
, 分别是左右焦点,且焦距为2
分别是左右焦点,且焦距为2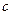 ,求△P
,求△P
 内切圆圆心横坐标。
内切圆圆心横坐标。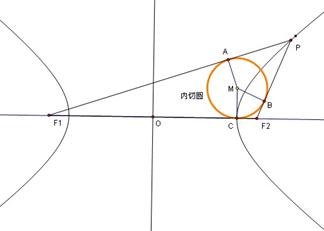
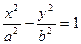 (
(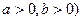 右支上的一点,
右支上的一点, ,
, 分别是左右焦点,且焦距为2
分别是左右焦点,且焦距为2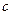 ,求△P
,求△P
 内切圆圆心横坐标。
内切圆圆心横坐标。
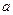
由双曲线第二定义知:P -P
-P =2
=2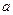 ,设切点分别为A,B,C
,设切点分别为A,B,C
由切线长相等得PA=PB, A=
A= C,
C,  B=
B= C
C
从而P -P
-P ="(" P
="(" P -PA)-(P
-PA)-(P -PB)=
-PB)= A-
A- B=
B= C-
C- C
C
即 C-
C- C=2
C=2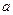 ,设C(
,设C(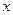 ,0),则
,0),则 C=
C=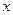 +
+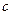 ,
, C=
C=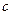 -
-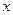
代入得(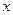 +
+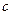 )-(
)-(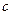 -
-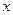 )=2
)=2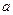 解得
解得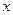 =
=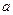 ,
,
即C点横坐标为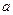 ,从而圆心M的横坐标为
,从而圆心M的横坐标为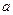
 -P
-P =2
=2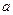 ,设切点分别为A,B,C
,设切点分别为A,B,C由切线长相等得PA=PB,
 A=
A= C,
C,  B=
B= C
C从而P
 -P
-P ="(" P
="(" P -PA)-(P
-PA)-(P -PB)=
-PB)= A-
A- B=
B= C-
C- C
C即
 C-
C- C=2
C=2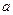 ,设C(
,设C(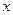 ,0),则
,0),则 C=
C=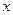 +
+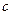 ,
, C=
C=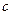 -
-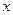
代入得(
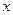 +
+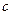 )-(
)-(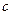 -
-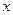 )=2
)=2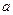 解得
解得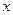 =
=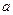 ,
,即C点横坐标为
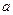 ,从而圆心M的横坐标为
,从而圆心M的横坐标为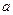

练习册系列答案
相关题目
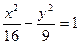 ,左焦点为
,左焦点为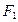 ,点
,点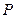 在双曲线右支上,求直线
在双曲线右支上,求直线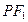 斜率范围
斜率范围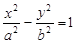 的焦点到渐近线的距离为
的焦点到渐近线的距离为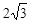 ,且双曲线右支上一点
,且双曲线右支上一点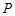 到右焦点的距离的最小值为2,则双曲线的离心率为( )
到右焦点的距离的最小值为2,则双曲线的离心率为( )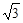
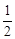
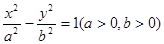 的离心率为
的离心率为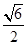 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为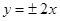 B.
B.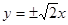 C.
C.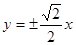 D.
D.
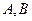 分别是射线
分别是射线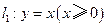 ,
,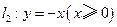 上的动点,
上的动点,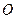 为坐标原点,且
为坐标原点,且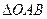 的面积为定值2.
的面积为定值2.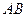 中点
中点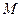 的轨迹
的轨迹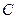 的方程;
的方程;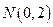 作直线
作直线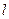 ,与曲线
,与曲线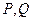 ,与射线
,与射线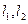 分别交于点
分别交于点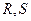 ,若点
,若点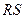 的两个三等分点,求此时直线
的两个三等分点,求此时直线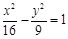 的焦距为
的焦距为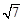
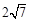
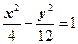 上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是__________
上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是__________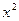 +4
+4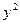 =16有相同的焦点,且一条渐近线为
=16有相同的焦点,且一条渐近线为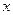 +
+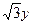 =0的双曲线的方程是: .
=0的双曲线的方程是: .