题目内容
【题目】已知函数
为偶函数，
．
（1）求实数
的值；
（2）若
时，函数
的图像恒在
图像的下方，求实数
的取值范围；
（3）当
时，求函数
在
上的最小值
．
【答案】（1）
（2）
（3）
【解析】
（1）利用函数是偶函数，建立方程进行求解即可（2）将不等式转化为
恒成立，利用参数分离法进行求解即可（3）利用换元法结合指数的性质，转化为一元二次函数，结合函数单调区间和对称轴的关系进行求解即可．
（1）
函数
为偶函数，
，
，
得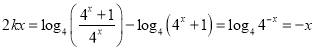
，
解得
，即
.
（2）若
时，函数
的图像恒在
图像的下方，
则恒成立，
即
，
即
，
化简得
，
即
恒成立，
在
上单调递减，
当
时，函数取得最大值
，
，
（3）当
时，
函数
，
设
，
，
，
则设
，
函数的对称轴为
，
，
，
若
，即
时，则函数在
上的最小值
，
若
，即
时，则函数在上的最小值
，
综上函数在
上的最小值.
练习册系列答案
相关题目
【题目】为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
（1）请将上面的列联表补充完整;
（2）能否在犯错概率不超过
的前提下认为喜好体育运动与性别有关?说明你的理由.
(参考公式: 
)
临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
