题目内容
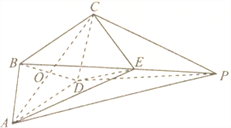
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .设
.设![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点.
中点.
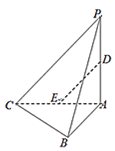
(1)求证:![]()
![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
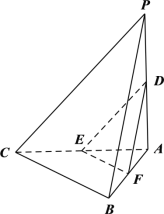
(3)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得过三点
,使得过三点![]() ,
,![]() ,
,![]() 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面![]() 平行?若存在,指出点
平行?若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)点![]() 是线段
是线段![]() 中点
中点
【解析】
(1)通过证明![]() ,证明
,证明![]() 平面
平面![]() ;
;
(2)通过![]() 和平面
和平面![]() 内的两条相交直线垂直,证明
内的两条相交直线垂直,证明![]() 平面
平面![]() ;
;
(3)通过证明两个平面内的两条相交直线分别平行,证明平面![]() 平面
平面![]() 即可.
即可.
(1)因为点![]() 是
是![]() 中点, 点
中点, 点![]() 为
为![]() 的中点,
的中点,
所以![]() ,又因为
,又因为![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]()
又因为![]() ,
,
所以![]() 平面
平面![]() ;
;
(3)当点![]() 是线段
是线段![]() 中点时,
中点时,
过点![]() 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面![]() 平行,证明如下:
平行,证明如下:
取![]() 中点
中点![]() ,连
,连![]() .
.
由(1)可知![]() 平面
平面![]() .
.
因为点![]() 是
是![]() 中点,点
中点,点![]() 为
为![]() 的中点,
的中点,
所以![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
所以平面![]() 内的任一条直线都与平面
内的任一条直线都与平面![]() 平行.
平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某地区不同身高的未成年男性的体重平均值如下表.
身高/ | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
体重/ | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 | 38.85 | 47.25 | 55.05 |
(1)根据表格提供的数据,能否建立恰当的函数模型,使它能比较近似地反映这个地区未成年男性体重![]() 与身高
与身高![]() 的函数关系?试写出这个函数模型的关系式.
的函数关系?试写出这个函数模型的关系式.
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为![]() ,体重为
,体重为![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?