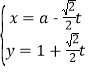题目内容

【题目】某地区不同身高的未成年男性的体重平均值如下表.

身高/

60

70

80

90

100

110

120

130

140

150

160

170

体重/

6.13

7.90

9.99

12.15

15.02

17.50

20.92

26.86

31.11

38.85

47.25

55.05

（1）根据表格提供的数据，能否建立恰当的函数模型，使它能比较近似地反映这个地区未成年男性体重与身高的函数关系？试写出这个函数模型的关系式.

（2）若体重超过相同身高男性体重平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么这个地区一名身高为，体重为的在校男生的体重是否正常？

【答案】（1）；（2）这个男生偏胖.

【解析】

（1）画出散点图，考虑作为函数模型，代入数据计算得到答案.

（2）根据函数解析式，代入数据得到，计算得到答案.

（1）以身高为横坐标，体重为纵坐标，画出散点图，

根据点的分布特征，可考虑以作为刻画这个地区未成年男性的体重与身高关系的函数模型.

取其中的两组数据，，代入得：

用计算器算得，.

这样，我们就得到一个函数模型：.

将已知数据代入上述函数关系式，或作出上述函数的图像，可以发现，这个函数模型与已知数据的拟合程度较好，这说明它能较好地反映这个地区未成年男性体重与身高的关系.

（2）将代入，得，由计算器算得.

由于，所以，这个男生偏胖.

练习册系列答案
相关题目

【题目】已知函数f(x)＝x2－mlnx，h(x)＝x2－x＋a.

(1)当a＝0时，f(x)≥h(x)在(1，＋∞)上恒成立，求实数m的取值范围；

(2)当m＝2时，若函数k(x)＝f(x)－h(x)在区间(1,3)上恰有两个不同零点，求实数a的取值范围．

【题目】如图，△ABC和△BCD所在平面互相垂直，且AB＝BC＝BD＝2，∠ABC＝∠DBC＝120°，E，F分别为AC，DC的中点．

(1)求证：EF⊥BC；

(2)求二面角E－BF－C的正弦值．

【题目】已知函数.

（1）时，求在上的单调区间；

（2）且， 均恒成立，求实数的取值范围.

【题目】如图，在三棱锥中，平面平面，，．设，分别为，中点．

（1）求证：平面；

（2）求证：平面；

（3）试问在线段上是否存在点，使得过三点，，的平面内的任一条直线都与平面平行？若存在，指出点的位置并证明；若不存在，请说明理由．

【题目】按照《国务院关于印发“十三五”节能减排综合工作方案的通知》（国发〔2016〕74号）的要求，到2020年，全国二氧化硫排放总量要控制在1580万吨以内，要比2015年下降15%.假设“十三五”期间每一年二氧化硫排放总量下降的百分比都相等，2015年后第年的二氧化硫律放总量最大值为万吨.

（1）求的解析式；

（2）求2019年全国二氧化赖持放总量要控制在多少万晚以内（精确到1万吨）.

【题目】某理财公司有两种理财产品A和B，这两种理财产品一年后盈亏的情况如下（每种理财产品的不同投资结果之间相互独立）：

产品A

投资结果

获利40%

不赔不赚

亏损20%

概率

产品B

投资结果

获利20%

不赔不赚

亏损10%

概率

p

q

注：p＞0，q＞0

（1）已知甲、乙两人分别选择了产品A和产品B投资，如果一年后他们中至少有一人获利的概率大于，求实数p的取值范围；

（2）若丙要将家中闲置的10万元人民币进行投资，以一年后投资收益的期望值为决策依据，则选用哪种产品投资较理想？

【题目】在平面直角坐标系中，曲线过点，其参数方程为（为参数，），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为．

（1）写出曲线的普通方程和曲线的直角坐标方程；

（2）已知曲线和曲线交于两点（在之间），且，求实数的值．

【题目】某商品促销活动设计了一个摸奖游戏：在一个口袋中装有4个红球和6个白球，这些球除颜色外完全相同，顾客一次从中摸出3个球，若3个都是白球则无奖励，若有1个红球则奖励10元购物券，若有2个红球则奖励20元购物券，若3个都是红球则奖励30元购物券.

（Ⅰ）求中奖的概率；

（Ⅱ）求顾客摸奖一次获得购物券奖励的平均值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网