题目内容
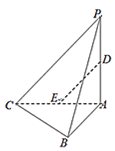
【题目】如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E、F分别是PC、AD中点,
(1)求证:DE//平面PFB;
(2)求PB与面PCD所成角的正切值。

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)取PB的中点G,连接EG,FG,通过证明四边形FGED是平行四边形,得ED//GF,进而可以得到DE//面PFB;
(2)先由条件求出∠BPC就是PB与面PCD所成的角,再通过求三角形边长即可得到结论
(1)取PB的中点G,连接EG,FG,如图,
![]() E,G分别是PC,PB的中点,
E,G分别是PC,PB的中点,
![]() FG//BC且FG=
FG//BC且FG=![]() BC,又DF//BC且DF=
BC,又DF//BC且DF=![]() BC
BC
![]() FG//DF且FG=DF,
FG//DF且FG=DF,
![]() 四边形FGED是平行四边形,
四边形FGED是平行四边形,
则DE//GF,又DE![]() 面PFB,GF
面PFB,GF![]() 面PFB,
面PFB,
![]() DE//面PFB
DE//面PFB
(2)由已知得:PD⊥面ABCD
∴PD⊥BC
∵ABCD是正方形
∴BC⊥CD
又PD∩CD=D
∴BC⊥面PCD
∴PB在面PCD内的射影是PC
∴∠BPC就是PB与面PCD所成的角.
设PD=DC=a,则PC=![]()
∴在△PBC中,∠PCB=90°,PC=![]() ,BC=a
,BC=a
∴tan∠BPC=![]()
∴PC与面PCD所成角的正切值为![]()

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表:
温度x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵个数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
(I)根据散点图判断,![]() 与
与![]() 哪一个适宜作为产卵数
哪一个适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(II)根据(I)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)红铃虫是棉区危害较重的害虫,可从农业、物理和化学三个方面进行防治,其中农业方面防治有3种方法,物理方面防治有1种方法,化学方面防治3种方法,现从7种方法中选3种方法进行综合防治(即3种方法不能全部来自同一方面,至少来自两个方面),X表示在综合防治中农业方面的防治方法的种数,求X的分布列及数学期望E(X).
附:可能用到的公式及数据表中(表中![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() )
)
|
|
|
|
|
|
|
27.430 | 3.612 | 81.290 | 147.700 | 2763.764 | 705.592 | 40.180 |
对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]()

【题目】某理财公司有两种理财产品A和B,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品A
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
产品B
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
| q |
注:p>0,q>0
(1)已知甲、乙两人分别选择了产品A和产品B投资,如果一年后他们中至少有一人获利的概率大于![]() ,求实数p的取值范围;
,求实数p的取值范围;
(2)若丙要将家中闲置的10万元人民币进行投资,以一年后投资收益的期望值为决策依据,则选用哪种产品投资较理想?