题目内容
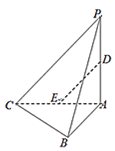
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 与
与![]() 的交点,
的交点, ![]() 为棱
为棱![]() 上一点.
上一点.
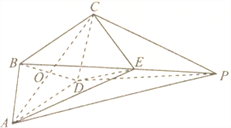
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,三棱锥
,三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)6.
【解析】试题分析:(1)由已知条件得出![]() 平面
平面![]() 平面EAC,由面面垂直的判定定理得出平面
平面EAC,由面面垂直的判定定理得出平面![]() 平面
平面![]() ;(2)由线面平行的性质得出E是PB的中点,取
;(2)由线面平行的性质得出E是PB的中点,取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明出
,证明出![]() 平面
平面![]() ,再由等体积法求出
,再由等体积法求出![]() 的值。
的值。
试题解析:
(1)因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
又四边形![]() 为菱形,所以
为菱形,所以![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
所以![]() .又
.又![]() 为
为![]() 与
与![]() 的交点,
的交点,
所以![]() 是
是![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中点.
的中点.
因为四边形![]() 是菱形,且
是菱形,且![]() ,
,
所以取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
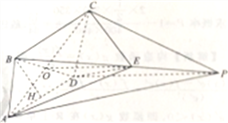
可知![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,
,
所以![]() 平面
平面![]() .
.
由于![]() ,所以
,所以![]() .
.
因此![]() 到平面
到平面![]() 的距离
的距离![]() ,
,
所以![]() .
.
解得![]() ,故
,故![]() 的值为
的值为![]() .
.

【题目】一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表:
温度x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵个数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
(I)根据散点图判断,![]() 与
与![]() 哪一个适宜作为产卵数
哪一个适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(II)根据(I)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)红铃虫是棉区危害较重的害虫,可从农业、物理和化学三个方面进行防治,其中农业方面防治有3种方法,物理方面防治有1种方法,化学方面防治3种方法,现从7种方法中选3种方法进行综合防治(即3种方法不能全部来自同一方面,至少来自两个方面),X表示在综合防治中农业方面的防治方法的种数,求X的分布列及数学期望E(X).
附:可能用到的公式及数据表中(表中![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() )
)
|
|
|
|
|
|
|
27.430 | 3.612 | 81.290 | 147.700 | 2763.764 | 705.592 | 40.180 |
对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]()

【题目】现从某医院中随机抽取了七位医护人员的关爱患者考核分数(患者考核: ![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:
表示;医护专业知识考核分数(试卷考试: ![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到
的线性回归方程(计算结果精确到![]() );
);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为![]() 分时,他的关爱患者考核分数(精确到
分时,他的关爱患者考核分数(精确到![]() );
);
(3)现要从医护专业知识考核分数![]() 分以下的医护人员中选派
分以下的医护人员中选派![]() 人参加组建的“九寨沟灾后医护小分队”培训,求这两人中至少有一人考核分数在
人参加组建的“九寨沟灾后医护小分队”培训,求这两人中至少有一人考核分数在![]() 分以下的概率.
分以下的概率.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为 ,
, ![]() .
.