题目内容
16.已知f(x)=x2+(a+1)x+b,f(3)=3,其中a,b∈R(1)若f(x)≥x对任意实数x恒成立,求a,b的值.
(2)求关于x的不等式f(x)>-9-4a的解集.
分析 (1)运用二次函数的性质,可得判别式小于等于0,解不等式可得a,b的值;
(2)化简不等式f(x)>-9-4a,可得(x+a)(x+1)>0,对a讨论,分a=1,a>1,a<1三种情况,可得不等式的解集.
解答 解:(1)f(3)=3,可得3a+b=-9.
f(x)≥x即为x2+ax+b≥0,
则x2+ax+b≥0对任意实数x恒成立,
即有△=a2-4b=a2-4(-9-3a)=(a+6)2≤0,
由(a+6)2≥0,即有a+6=0,
解得a=-6,b=9;
(2)不等式f(x)>-9-4a,即为
x2+(a+1)x-9-3a>-9-4a,
即有x2+(a+1)x+a>0,
即(x+a)(x+1)>0,
当a=1时,(x+1)2>0,原不等式的解集为{x|x≠-1};
当a>1时,-a<-1,原不等式的解集为{x|x>-1或x<-a};
当a<1时,-a>-1,原不等式的解集为{x|x>-a或x<-1}.
点评 本题考查二次不等式恒成立问题的解法,同时考查二次不等式的解法,注意运用分类讨论的思想方法,属于中档题.

练习册系列答案
相关题目
6.如图⊙O中,弦AB与弦CD相交于点P,∠B=38°,∠APD=80°,则∠A等于( )
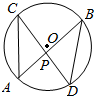

| A. | 38° | B. | 42° | C. | 80° | D. | 118° |
4.把13个相同的球全部放入编号为1、2、3的三个盒内,要求盒内的球数不小于盒号数,则不同的放入方法种数为( )
| A. | 36 | B. | 45 | C. | 66 | D. | 78 |
1.记anan-1…a1a0(k)) 表示一个k进制数,若21(k)=9(10),则321(k)在十进制中所表示的数为( )
| A. | 86 | B. | 57 | C. | 34 | D. | 17 |
8.iPhone 6是苹果公司(Apple)在2014年9月9日推出的一款手机,已于9月19日正式上市.据统计发现该产品的广告费用x与销售额y的统计数据如表:
根据上表可得回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\stackrel{∧}{b}$为9.4,据此模型预报广告费用为6百万元时销售额为( )
| 广告费用x(百万元) | 4 | 2 | 3 | 5 |
| 销售额y(百万元) | 44 | 25 | 37 | 54 |
| A. | 61.5百万元 | B. | 62.5百万元 | C. | 63.5百万元 | D. | 65.0百万元 |
5.研究一下,满足以下两个要求的三角形:①三边是连续的三个自然数;②最大角是最小角的两倍.这样的三角形( )
| A. | 不存在 | B. | 可能是直角三角形 | ||
| C. | 必为钝角三角形 | D. | 可能是锐角三角形 |
6.在一次考试中,5名学生的数学和物理成绩如表:(已知学生的数学和物理成绩具有线性相关关系)
现已知其线性回归方程为$\stackrel{∧}{y}$=0.36$\stackrel{∧}{x}$+a,则根据此线性回归方程估计数学得80分的同学的物理成绩为70(四舍五入到整数)
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学成绩x | 80 | 75 | 70 | 65 | 60 |
| 物理成绩y | 70 | 66 | 68 | 64 | 62 |