如图.在等腰△ABC中.AB=AC=1.∠A=120°.则向量$\overrightarrow{BA}$在向量$\overrightarrow{BC}$上的投影等于( )A．-$\frac{\sqrt{3}}{2}$B．$\frac{\sqrt{3}}{2}$C．-$\frac{1}{2}$D．$\frac{1}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

13．如图，在等腰△ABC中，AB=AC=1，∠A=120°，则向量$\overrightarrow{BA}$在向量$\overrightarrow{BC}$上的投影等于（　　）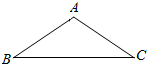

A．

-$\frac{\sqrt{3}}{2}$

B．

$\frac{\sqrt{3}}{2}$

C．

-$\frac{1}{2}$

D．

$\frac{1}{2}$

分析由题意可得∠ABC=30°，再根据一个向量在另一个向量上的投影的定义求得向量$\overrightarrow{BA}$在向量$\overrightarrow{BC}$上的投影．

解答解：由题意可得∠ABC=30°，∴向量$\overrightarrow{BA}$在向量$\overrightarrow{BC}$上的投影等于|$\overrightarrow{BA}$|•cos∠ABC=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$，
故选：B．

点评本题主要考查一个向量在另一个向量上的投影的定义，属于基础题．

练习册系列答案

4．在△ABC中，角A，B，C所对的边分别为a，b，c，若$\overrightarrow{m}$=（sinA，sinB），$\overrightarrow{n}$=（sinB，sinC），$\overrightarrow{m}$•$\overrightarrow{n}$=1-cos2B．
（1）求证：a，b，c成等差数列；
（2）若C=$\frac{2π}{3}$，求$\frac{a}{b}$的值．

1．求解下列关于x的不等式：
（1）|2x-1|≥3；
（2）|x-3|+|x+1|＜6．

8．已知等比数列{a_n}公比q＞1，若a₅-a₁=15，a₄-a₂=6，则a₃=（　　）

18．已知函数y=lg（mx²+2x+m-1）．
（1）若函数的定义域为R，求实数m的取值范围；
（2）若函数的定义域为M，且（0，3）⊆M，求m的取值范围．

5．正方形ABCD的边长为a，E，F分别是边AB，BC的中点，沿DE，EF，FD将△DAE，△EBF，△FCD折起来，三棱锥S-DEF的外接球的体积为$\frac{\sqrt{6}}{8}$πa³．

2．（1）求y=x+$\frac{1}{x-2}$（x＞2）得最小值．
（2）求（x+y）（$\frac{1}{x}$+$\frac{1}{y}$）的最小值，其中x＞0，y＞0．

3．已知数列{b_n}满足b₁=$\frac{3}{10}$，b_n+1=1-$\frac{1}{4{b}_{n}}$（n∈N^*），设a_n=$\frac{2}{1-2{b}_{n}}$
（1）求证：数列{a_n}是等差数列；
（2）数列{a${\;}_{{c}_{n}}$}为等比数列，且c₁=5，c₂=8，若对任意的n∈N^*都有k（2c_n-7）＜a_n成立，求实数k的取值范围．

试题分类