题目内容
5．正方形ABCD的边长为a，E，F分别是边AB，BC的中点，沿DE，EF，FD将△DAE，△EBF，△FCD折起来，三棱锥S-DEF的外接球的体积为$\frac{\sqrt{6}}{8}$πa3．分析 要求三棱锥的体积先找出可以应用的底面和对应的高，这里选择三角形SEF做底面，得到结果．
解答 解：由题意图形折叠为三棱锥，且由S出发的三条棱两两垂直，
边长分别为a，$\frac{a}{2}$，$\frac{a}{2}$，
可以SD，SE，SF为边补成长方体，
即有长方体的对角线即为球的直径，
则2r=$\sqrt{{a}^{2}+\frac{{a}^{2}}{4}+\frac{{a}^{2}}{4}}$=$\frac{\sqrt{6}}{2}$a，
r=$\frac{\sqrt{6}}{4}$a，
体积V=$\frac{4}{3}$πr3=$\frac{\sqrt{6}}{8}$πa3．
故答案为：$\frac{\sqrt{6}}{8}$πa3．
点评 本题是基础题，考查几何体的体积的求法，注意折叠问题的处理方法，考查计算能力
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
由于当前学生课业负担重，造成青少年视力普遍下降，现从某高中随机抽取16名学生，经校医用视力表检查得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶）如图：请指出这组数据的中位数为4.75．
13．如图，在等腰△ABC中，AB=AC=1，∠A=120°，则向量$\overrightarrow{BA}$在向量$\overrightarrow{BC}$上的投影等于（ ）
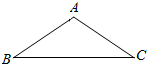
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
10．设实数x，y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y≤2\end{array}$，则u=$\frac{x+y}{x}$的取值范围是（ ）
| A． | $[{\frac{4}{3}，\frac{3}{2}}]$ | B． | $[{\frac{1}{3}，2}]$ | C． | $[{\frac{4}{3}，3}]$ | D． | $[{\frac{3}{2}，3}]$ |
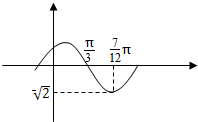函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，