题目内容
8．已知等比数列{an}公比q＞1，若a5-a1=15，a4-a2=6，则a3=（ ）| A． | -16 | B． | -4 | C． | 4 | D． | -4或4 |
分析 根据题意和等比数列的通项公式列出方程组，求出公比q和首项的值，再求出a3的值．
解答 解：∵a5-a1=15，a4-a2=6，且公比q＞1，
∴$\left\{\begin{array}{l}{{a}_{1}{q}^{4}-{a}_{1}=15}\\{{a}_{1}{q}^{3}-{a}_{1}q=6}\end{array}\right.$，解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{q=2}\end{array}\right.$，
∴a3=${a}_{1}{q}^{2}$=4，
故选：C．
点评 本题考查等比数列的通项公式，以及方程思想，属于基础题．
练习册系列答案
相关题目
由于当前学生课业负担重，造成青少年视力普遍下降，现从某高中随机抽取16名学生，经校医用视力表检查得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶）如图：请指出这组数据的中位数为4.75．
13．如图，在等腰△ABC中，AB=AC=1，∠A=120°，则向量$\overrightarrow{BA}$在向量$\overrightarrow{BC}$上的投影等于（ ）
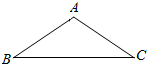
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
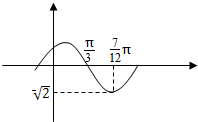函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，