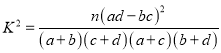题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是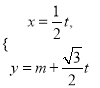 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上运动,若
上运动,若![]() 的最小值为1,求
的最小值为1,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1) 先利用两角差的余弦公式展开后,两边同乘以![]() ,利用
,利用![]() ,
, ![]() 把极坐标方程化为直角坐标方程;(2)把圆的方程配方化为标准方程,得出圆心和半径,把直线方程
把极坐标方程化为直角坐标方程;(2)把圆的方程配方化为标准方程,得出圆心和半径,把直线方程![]() 的参数方程消去参数化为普通方程,求出圆心到直线的距离减去圆的半径就是
的参数方程消去参数化为普通方程,求出圆心到直线的距离减去圆的半径就是![]() 的最小值,令其得1,解方程得出求
的最小值,令其得1,解方程得出求![]() 的值.
的值.
试题解析:
(1)![]() ,即
,即![]() ,所以
,所以![]() ,将
,将![]() ,
, ![]() ,
, ![]() 代入得
代入得![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)将![]() 化为
化为![]() ,所以
,所以![]() 是圆心为
是圆心为![]() ,半径为2的圆,将
,半径为2的圆,将![]() 的参数方程化为普通方程为
的参数方程化为普通方程为![]() ,所以
,所以
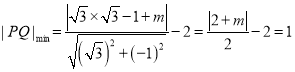 ,由此解得
,由此解得![]() 或
或![]() .
.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案【题目】近年来许多地市空气污染较为严重,现随机抽取某市一年(365天)内100天的![]() 空气质量指数(
空气质量指数(![]() )的监测数据,统计结果如表:
)的监测数据,统计结果如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 4 | 13 | 18 | 30 | 20 | 15 |
记某企业每天由空气污染造成的经济损失为![]() (单位:元),
(单位:元),![]() 指数为
指数为![]() .当
.当![]() 在区间
在区间![]() 内时,对企业没有造成经济损失;当
内时,对企业没有造成经济损失;当![]() 在区间
在区间![]() 内时,对企业造成的经济损失与
内时,对企业造成的经济损失与![]() 成直线模型(当
成直线模型(当![]() 指数为150时,造成的经济损失为1100元,当
指数为150时,造成的经济损失为1100元,当![]() 指数为200时,造成的经济损失为1400元);当
指数为200时,造成的经济损失为1400元);当![]() 指数大于300时,造成的经济损失为2000元.
指数大于300时,造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取1天,该天经济损失![]() 大于1100且不超过1700元的概率;
大于1100且不超过1700元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,这30天中有8天为严重污染,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该市本年度空气严重污染与供暖有关?
的把握认为该市本年度空气严重污染与供暖有关?
非严重污染 | 严重污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 |
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中![]()
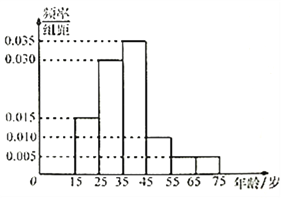
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在![]() 岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为:
岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .把年龄落在区间
.把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年”和“中老年”.
内的人分别称为“青少年”和“中老年”.
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数
(2)根据已知条件完成下面的2×2列联表,并判断能否有99%的把握认为关注“带一路”是否和年龄段有关?
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
附:参考公式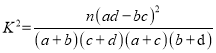 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |