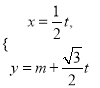题目内容
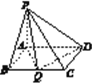
【题目】如图所示, ![]() 与四边形
与四边形![]() 所在平面垂直,且
所在平面垂直,且![]() .
.

(1)求证: ![]() ;
;
(2)若![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求
,求![]() .
.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)由三角形全等即等腰三角形的性质可得![]() 由线面垂直的性质可得
由线面垂直的性质可得 ![]() ,从而
,从而![]() 平面
平面![]() ,由此能证明
,由此能证明![]() .(2)分别以
.(2)分别以![]() 所在直线为
所在直线为![]() 轴,过
轴,过![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的一个法向量及直线
的一个法向量及直线![]() 的方向向量,根据空间向量夹角余弦公式及同角三角函数之间的关系,可得结果.
的方向向量,根据空间向量夹角余弦公式及同角三角函数之间的关系,可得结果.
试题解析:(1)证明:由PA⊥平面ABCD,AB=AD,可得PB=PD,
又BC=CD,PC=PC,所以△PBC≌△PDC,所以∠PBC=∠PDC.
因为PD⊥DC,所以PB⊥BC.3分
因为PA⊥平面ABCD,BC平面ABCD,
所以PA⊥BC.
又PA∩PB=P,所以BC⊥平面PAB.
因为AB平面PAB,所以AB⊥BC.5分
(2)由BD=BC=CD,AB⊥BC,可得∠ABD=30°,
又已知AB=AD,BD=PA=![]() ,所以AB=1.
,所以AB=1.
如图所示,分别以BC,BA所在直线为x,y轴,过B且平行于PA的直线为z轴建立空间直角坐标系,
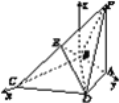
则B(0,0,0),P(0,1, ![]() ),C(
),C(![]() ,0,0),E(
,0,0),E(![]() ,
, ![]() ,
, ![]() ),D(
),D(![]() ,
, ![]() ,0),所以
,0),所以![]() =(
=(![]() ,
, ![]() ,-
,- ![]() ),
), ![]() =(
=(![]() ,
, ![]() ,
, ![]() ),
), ![]() =(
=(![]() ,
, ![]() ,0).
,0).
设平面BDE的法向量n=(x,y,z),
则![]() ,即
,即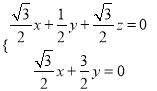 取z=-2,得n=(3,-
取z=-2,得n=(3,- ![]() ,-2),
,-2),
所以sin θ=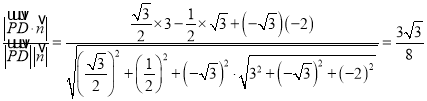 .
.

练习册系列答案
相关题目