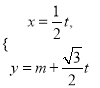Question

【题目】椭圆C： 的左、右顶点分别为A1、A2，点P在C上且直线PA2的斜率的取值范围是[－2，－1]，那么直线PA1斜率的取值范围是________.

Answer 1

【答案】

【解析】由题意可得，A1(－2,0)，A2(2,0)，

当PA2的斜率为－2时，直线PA2的方程为y＝－2(x－2)，

代入椭圆方程，消去y化简得19x2－64x＋52＝0，

解得x＝2或x＝.

由PA2的斜率存在可得点P，

此时直线PA1的斜率k＝.

同理，当直线PA2的斜率为－1时，

直线PA2的方程为y＝－(x－2)，

代入椭圆方程，消去y化简得7x2－16x＋4＝0，解得x＝2或x＝

由PA2的斜率存在可得点P，

此时直线PA1的斜率k＝.

数形结合可知，直线PA1斜率的取值范围是