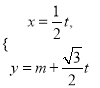题目内容
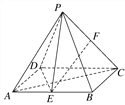
【题目】如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且tan∠EAB=![]() .
.
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD⊥平面ADE;
(3)在CD上是否存在一点M,使得MO∥平面ADE,证明你的结论.

【答案】详见解析
【解析】试题分析:(1)因为![]() 是三棱锥的高,因此计算
是三棱锥的高,因此计算![]() 可以转化
可以转化![]() 来计算.(2)中的面面垂直的证明可以归结为
来计算.(2)中的面面垂直的证明可以归结为![]() 平面
平面![]() ,后者可由
,后者可由![]() 得到.(3)要证明
得到.(3)要证明![]() 平面
平面![]() ,可取为
,可取为![]() 的中点为
的中点为![]() ,通过证明平面
,通过证明平面![]() 平面
平面![]() 得到.
得到.
解析: (1)∵![]() 是圆柱的母线,∴
是圆柱的母线,∴![]() 平面
平面![]() ,∴
,∴![]() 为三棱锥
为三棱锥![]() 的高,又∵
的高,又∵![]() ,
, ![]() ,∴
,∴![]() .又∵
.又∵![]() 为圆
为圆![]() 的直径,∴
的直径,∴![]() ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(2)∵![]() 平面
平面![]() ,∴
,∴![]() .又∵
.又∵![]() ,∴
,∴![]() 平面
平面![]() ,又∵四边形
,又∵四边形![]() 为矩形,∴
为矩形,∴![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(3)在![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() 为
为![]() 的中点,证明如下:
的中点,证明如下:
取![]() 的中点
的中点![]() ,连接
,连接![]() .∵
.∵![]() 分别为
分别为![]() 的中点,∴
的中点,∴![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,同理
,同理![]() 平面
平面![]() .∵
.∵![]() ,∴平面
,∴平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.


练习册系列答案
相关题目