题目内容
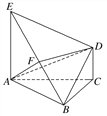
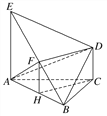
【题目】如图所示,底面ABC为正三角形,EA⊥平面ABC,DC⊥平面ABC,EA=AB=2DC=2a,设F为EB的中点.
(1)求证:DF∥平面ABC;
(2)求直线AD与平面AEB所成角的正弦值.
【答案】(1)见解析;(2) ![]()
【解析】试题分析:(1)过点F作FH∥EA交AB于点H,根据平几知识可得CDFH是平行四边形,即得DF∥CH,再根据线面平行判定定理得结论(2)先根据正三角形性质得CH⊥AB,再根据线面垂直判定定理得CH⊥平面AEB,即得DF⊥平面AEB,从而∠DAF为直线AD与平面AEB所成的角.最后解直角三角形得直线AD与平面AEB所成角的正弦值.
试题解析:(1)证明 如图,过点F作FH∥EA交AB于点H,连接HC.
∵EA⊥平面ABC,DC⊥平面ABC,
∴EA∥DC.
又FH∥EA,
∴FH∥DC.
∵F是EB的中点,
∴FH=![]() AE=DC.
AE=DC.
∴四边形CDFH是平行四边形,
∴DF∥CH.
又CH平面ABC,DF平面ABC,
∴DF∥平面ABC.
(2)解 ∵△ABC为正三角形,H为AB的中点,∴CH⊥AB.
∵EA⊥平面ABC,CH平面ABC,
∴CH⊥EA.
又EA∩AB=A,EA平面AEB,
AB平面AEB,
∴CH⊥平面AEB.
∵DF∥CH,
∴DF⊥平面AEB,
∴AF为DA在平面AEB上的投影,
∴∠DAF为直线AD与平面AEB所成的角.
在Rt△AFD中,AD=![]() a,DF=
a,DF=![]() a,sin∠DAF=
a,sin∠DAF=![]() =
=![]() ,
,
∴直线AD与平面AEB所成角的正弦值为![]() .
.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目