题目内容
(本小题满分12分)已知直线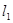 的方程为
的方程为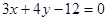 ,求满足下列条件的直线
,求满足下列条件的直线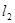 的方程.
的方程.
(1)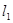 与
与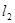 平行且过点(-1,3)
平行且过点(-1,3)
(2)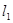 与
与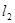 垂直且与两坐标轴围成的三角形面积为4.
垂直且与两坐标轴围成的三角形面积为4.
(1)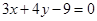 ;(2)
;(2) 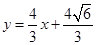 或
或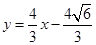
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
(本小题满分12分)已知直线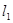 的方程为
的方程为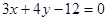 ,求满足下列条件的直线
,求满足下列条件的直线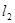 的方程.
的方程.
(1)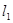 与
与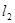 平行且过点(-1,3)
平行且过点(-1,3)
(2)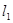 与
与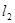 垂直且与两坐标轴围成的三角形面积为4.
垂直且与两坐标轴围成的三角形面积为4.
(1)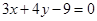 ;(2)
;(2) 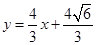 或
或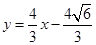
解析

 名校课堂系列答案
名校课堂系列答案