题目内容
(本小题满分8分)已知直线l垂直于直线3x-4y-7=0,直线l与两坐标轴围成的三角形的周长为10,求直线l的方程
解:设直线l方程为4x+3y+b=0, ------------------1分
则l与?x轴、y轴的交点为A(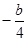 ,0),B(0,
,0),B(0,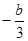 ).---------- 3分
).---------- 3分
∴|AB|=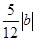 . ---------------------- 4分
. ---------------------- 4分
由|OA|+|OB|+|AB|=10,
得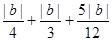 =10.∴b=±10. ------------------- 7分
=10.∴b=±10. ------------------- 7分
∴l方程为4x+3y+10=0,4x+3y-10=0. ------8分
解析试题分析:因为直线l垂直于直线3x-4y-7=0,所以设直线l方程为4x+3y+b=0,再分别求出A,B点的坐标,利用两点间距离公式求出三角形ABO的三边长,根据三角形ABO的周长为10,就可得到参数B的值,求得直线l的方程.
考点:本题主要是考查互相垂直的两直线方程之间的关系,以及待定系数法求直线方程
点评:解决该试题的关键是利用垂直关系,设直线l方程为4x+3y+b=0,再分别求出A,B点的坐标,和三角形ABO的三边长。

练习册系列答案
相关题目
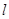 的参数方程为
的参数方程为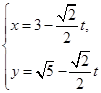 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为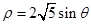 。
。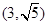 ,求|PA|+|PB|。
,求|PA|+|PB|。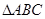 的三个顶点
的三个顶点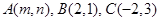 .
.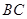 边所在直线方程;
边所在直线方程;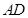 的方程为
的方程为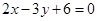 ,且
,且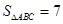 ,求
,求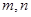 的值.
的值.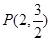 的直线
的直线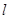 与
与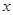 轴的正半轴、
轴的正半轴、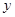 轴的正半轴分别交于点
轴的正半轴分别交于点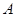 、
、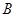 ,
,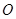 为坐标原点,
为坐标原点,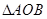 的面积等于6,求直线
的面积等于6,求直线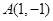 向直线
向直线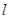 作垂线,垂足为
作垂线,垂足为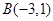 .求直线
.求直线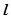 : x+2y+2=0
: x+2y+2=0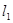 的方程为
的方程为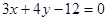 ,求满足下列条件的直线
,求满足下列条件的直线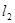 的方程.
的方程. 3)且在
3)且在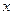 轴的截距与它在y轴上的截距的和为零.
轴的截距与它在y轴上的截距的和为零.