题目内容
【题目】已知函数f(x)=x2+2ax+a2﹣1.
(1)若对任意的x∈R均有f(1﹣x)=f(1+x),求实数a的值;
(2)当x∈[﹣1,1]时,求f(x)的最小值,用g(a)表示其最小值,判断g(a)的奇偶性.
【答案】
(1)解:∵函数f(x)=x2+2ax+a2﹣1对任意的实数x都有f(1+x)=f(1﹣x)成立,
∴函数的对称轴x=﹣a=1,
∴a=﹣1
(2)解:∵f(x)=x2+2ax+a2﹣1=(x+a)2﹣1,其对称轴为x=﹣a,
当﹣a≤﹣1时,即a≥1时,函数f(x)在[﹣1,1]上单调递增,故g(a)=f(x)min=f(﹣1)=a2﹣2a,
当﹣1<﹣a<1时,即﹣1<a<1时,故g(a)=f(x)min=f(a)=﹣1,
当﹣a≥1时,即a≤﹣1时,函数f(x)在[﹣1,1]上单调递减,故g(a)=f(x)min=f(1)=a2+2a,
∴g(a)= 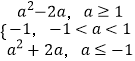 ,
,
∵g(﹣a)=g(a),
∴g(a)为偶函数
【解析】1、由二次函数的性质可得对任意的实数x都有f(1+x)=f(1﹣x)成立,函数的对称轴x=﹣a=1,∴a=﹣1。
2、由二次函数的图象和性质,当﹣a≤﹣1时,即a≥1时,函数f(x)在[﹣1,1]上单调递增,故g(a)=f(x)min=f(﹣1)=a2﹣2a
当﹣1<﹣a<1时,即﹣1<a<1时,故g(a)=f(x)min=f(a)=﹣1,当﹣a≥1时,即a≤﹣1时,函数f(x)在[﹣1,1]上单调递减,故g(a)=f(x)min=f(1)=a2+2a,得出函数的解析式,由偶函数定义可证。
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案