题目内容
【题目】已知圆O为Rt△ABC的外接圆,AB=AC,BC=4,过圆心O的直线l交圆O于P,Q两点,则 ![]() 的取值范围是( )
的取值范围是( )
A.[﹣8,﹣1]
B.[﹣8,0]
C.[﹣16,﹣1]
D.[﹣16,0]
【答案】B
【解析】解:以O为坐标原点,BC所在的直线为x轴,BC的中垂线为y轴, 建立直角坐标系,如图所示;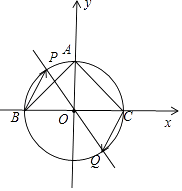
在Rt△ABC中,AB=AC,BC=4,
所以△ABC的外接圆圆心是BC的中点,半径为r= ![]() BC=2,
BC=2,
所以A(0,2),B(﹣2,0),C(2,0),
圆O的方程为:x2+y2=4;
当直线PQ的斜率不存在时,有P(0,2),Q(0,﹣2),![]() =(2,2),
=(2,2), ![]() =(﹣2,﹣2),则
=(﹣2,﹣2),则 ![]() =﹣4﹣4=﹣8;
=﹣4﹣4=﹣8;
当直线PQ的斜率存在时,设直线l为:y=kx,
代入圆的方程可得P(﹣ ![]() ,﹣
,﹣ ![]() ),Q(
),Q( ![]() ,
, ![]() ),
),
则 ![]() =(2﹣
=(2﹣ ![]() ,﹣
,﹣ ![]() ),
), ![]() =(
=( ![]() ﹣2,
﹣2, ![]() ),
),
所以 ![]() =(2﹣
=(2﹣ ![]() )(
)( ![]() ﹣2)+(﹣
﹣2)+(﹣ ![]() )
) ![]()
=﹣8+ ![]() ,
,
由1+k2≥1可得0< ![]() ≤8,
≤8,
所以﹣8<﹣8+ ![]() ≤0;
≤0;
综上, ![]() 的取值范围是[﹣8,0].
的取值范围是[﹣8,0].
故选:B.

练习册系列答案
相关题目