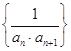题目内容
【题目】给出下列四种说法:①函数![]() 的单调递增区间是
的单调递增区间是![]() ;②函数
;②函数![]() 与
与![]() 的值域相同;③函数
的值域相同;③函数![]() 与
与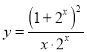 均是奇函数;④若函数
均是奇函数;④若函数![]() 在
在![]() 上有零点,则实数
上有零点,则实数![]() 的取值范围是
的取值范围是![]() .其中正确结论的序号是_______.
.其中正确结论的序号是_______.
【答案】③④
【解析】
根据对数函数的定义域,可判断①为假命题;分别求出![]() 与
与![]() 的值域,可判断②为假命题;由奇函数的定义即可判断③的真假;分离参数转化为
的值域,可判断②为假命题;由奇函数的定义即可判断③的真假;分离参数转化为![]() ,求出函数
,求出函数![]() 的值域,即可判定④的真假.
的值域,即可判定④的真假.
①函数![]() 有意义须
有意义须![]() ,
,
解得![]() 或
或![]() ,所以
,所以![]() 时,函数没意义,
时,函数没意义,
所以①错误;
②函数![]() 的值域为
的值域为![]() ,而
,而![]() 的值域为
的值域为![]() ,
,
所以②错误;
③函数![]() 与
与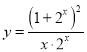 定义域均为
定义域均为![]() ,
,
令![]() ,
,
![]() ,
,
所以![]() 为奇函数,
为奇函数,
令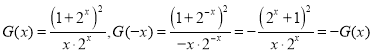
所以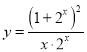 为奇函数,所以③正确;
为奇函数,所以③正确;
④令![]() 有零点,
有零点,
令![]() ,根据对勾函数性质可得,
,根据对勾函数性质可得,
![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,以下证明:
单调递增,以下证明:
设![]()
![]() ,
,
![]() ,
,
![]() 在
在![]() 单调递减,
单调递减,
同理![]() 在
在![]() 单调递增,所以
单调递增,所以![]() 的最小值为
的最小值为![]() ,
,
![]()
![]() 的最大值为
的最大值为![]() ,
,
要使![]() 有解,需
有解,需![]() ,
,
所以④正确.
故答案为:③④.

练习册系列答案
相关题目
【题目】某市预测2000年到2004年人口总数与年份的关系如下表所示
年份200x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十)万 | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,计算![]() ,用最小二乘法求出
,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
(2) 据此估计2005年该城市人口总数。
(参考数值:0×5+1×7+2×8+3×11+4×19=132,![]()
参考公式:用最小二乘法求线性回归方程系数公式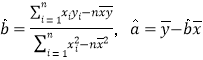 )
)